Rätselwochenende im November 2015
Wir hatten mal wieder viel Spaß miteinander. Unter anderem gab es diesmal viele Wettbewerbe: Eine Teamrunde, wie sie in der LM 2015 vorkam, Domino-Yinyang-Rätsel von der WM, eine Krypto-Runde, ein Wettbewerb, bei dem einige Rätsel mehrdeutig oder gar unlösbar waren und ein Design-Wettbewerb.
Bei letzterem hatten die Teilnehmer 30 Minuten Zeit um ein vorgegebenes Rätseldiagramm so zu erweitern, dass dabei ein eindeutig lösbares Rätsel herauskommt. Bis zu zwei Rätsel konnten die Teilnehmer abgeben. Diese wurden dann von einer Jury überprüft und bewertet. Und hier sind die Ergebnisse:
Gesamtwertung
- Platz 1: Claudia mit 36 Punkten
- Platz 2: Philipp mit 32 Punkten
- Platz 3: Jürgen mit 31 Punkten
Einzelwertung
- Platz 1: Claudias Hochhausvariante mit 20 Punkten
- Platz 2: Dandelos Fillomino mit 19 Punkten
- Platz 3: Gabis Höhle und Jürgens Doppelblock mit je 18 Punkten
Rätsel
Nachfolgend die Rätsel in der Reihenfolge, wie sie der Jury vorlagen.
- Minesweeper (Mody)
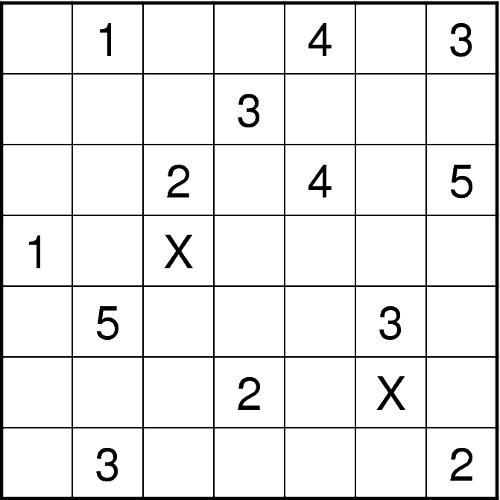
Platzieren Sie Minen so im Diagramm, dass die Zahlen angeben, wie viele der waagerecht, senkrecht und diagonal benachbarten Felder eine Mine enthalten. In Feldern mit Zahlen dürfen keine Minen platziert werden. Felder mit einem X sind ebenfalls leer. - Fillomino, nur Rechtecke (Rollo)
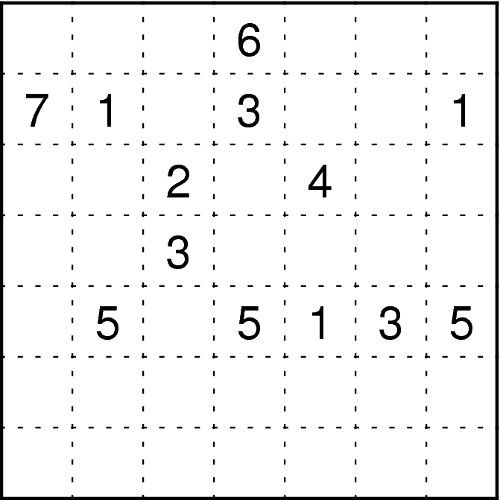
Unterteilen Sie das Diagramm in rechteckige Gebiete und schreiben Sie in jedes Feld eine Zahl. Die Zahlen in einem Gebiet müssen alle gleich sein und die Anzahl der Felder dieses Gebiets angeben. Gebiete gleicher Größe dürfen sich dabei waagerecht oder senkrecht nicht berühren, wohl aber diagonal. Vorgegebene Zahlen können zum gleichen Gebiet gehören und es kann Gebiete geben, von denen noch keine Zahl bekannt ist – auch mit größeren als den vorgegebenen Zahlen. - Fillomino (Dandelo)
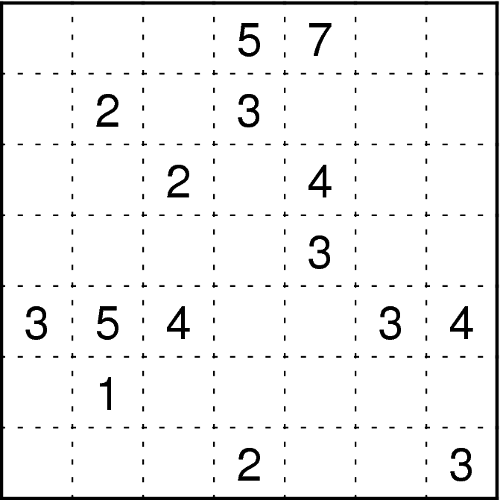
Unterteilen Sie das Diagramm in Gebiete und schreiben Sie in jedes Feld eine Zahl. Die Zahlen in einem Gebiet müssen alle gleich sein und die Anzahl der Felder dieses Gebiets angeben. Gebiete gleicher Größe dürfen sich dabei waagerecht oder senkrecht nicht berühren, wohl aber diagonal. Vorgegebene Zahlen können zum gleichen Gebiet gehören und es kann Gebiete geben, von denen noch keine Zahl bekannt ist – auch mit größeren als den vorgegebenen Zahlen. - Hochhausvariante (Claudia)
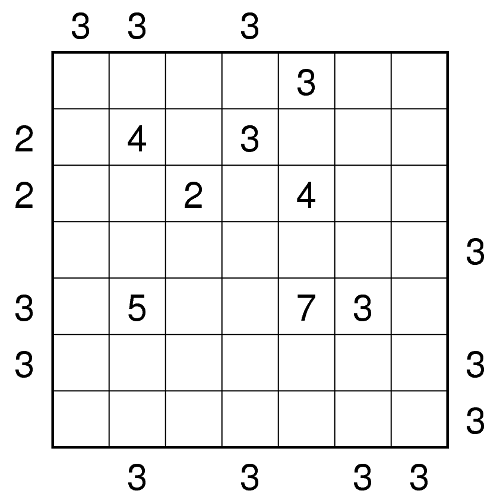
Tragen Sie in jedes Feld ein Hochhaus der Höhe 1 bis 7 so ein, dass in jeder Zeile und jeder Spalte jede mögliche Höhe genau einmal vorkommt. Die Zahlen am Rand geben jeweils an, wie viele Häuser in der entsprechenden Zeile oder Spalte aus der entsprechenden Richtung gesehen werden können; niedrigere Hochhäuser werden dabei von höheren verdeckt. Achtung: Es sind genau die Hinweise angegeben, die auf der entsprechenden Seite am häufigsten vorkommen.Im Nachhinein stellte sich das Rätsel als mehrlösig heraus. Das ist der Jury aber nicht aufgefallen. Um das Rätsel eindeutig zu bekommen, kann man in der dritten Zeile in das Feld ganz links eine 3 eintragen.
- Tapa (Jürgen)
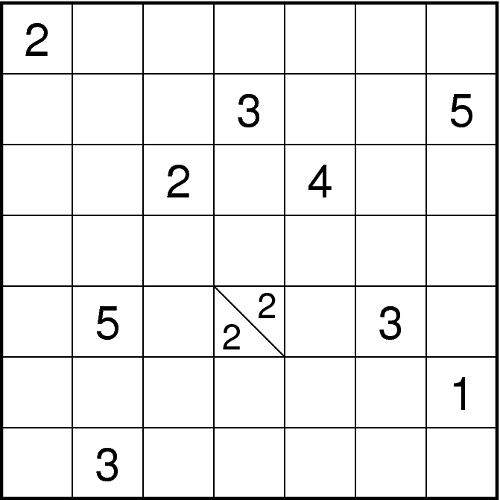
Schwärzen Sie einige der leeren Felder so, dass alle schwarzen Felder waagerecht und senkrecht zusammenhängen und kein 2x2-Bereich komplett geschwärzt ist. Felder mit Zahlen dürfen nicht geschwärzt werden. Die Zahlen geben an, wie viele der jeweiligen waagerecht, senkrecht und diagonal benachbarten Felder geschwärzt sind: Jede Zahl entspricht einer Gruppe aus waagerecht und senkrecht zusammenhängenden Schwarzfeldern, mehrere Gruppen sind dabei durch ein oder mehrere weiße Felder getrennt. Position und Reihenfolge der Zahlen in einem Feld spielen dabei keine Rolle. - Kropki (Claudia)

Tragen Sie Zahlen von 1 bis 7 so in das Diagramm ein, dass jede Zahl in jeder Zeile und jeder Spalte genau einmal vorkommt. Befindet sich zwischen zwei Feldern ein schwarzer Kreis, so muss eine der beiden Zahlen in diesen Feldern genau das Doppelte der anderen sein. Ein weißer Kreis hingegen bedeutet, dass eine der beiden Zahlen in diesen Feldern genau um eins größer sein muss als die andere. Befindet sich kein Kreis zwischen zwei Feldern, so darf keine der beiden Eigenschaften zutreffen. - Bosnian Road (Christian)
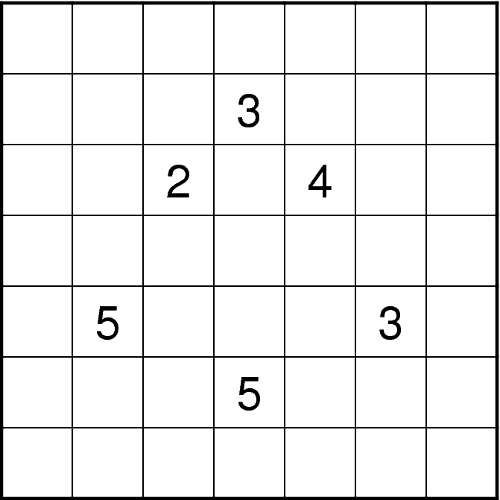
Zeichnen Sie in das Diagramm einen Rundweg ein, der waagerecht und senkrecht von Feldmittelpunkt zu Feldmittelpunkt verläuft. Der Rundweg muss nicht durch alle Felder gehen und darf nicht durch Felder mit Zahlen gehen. Die Zahlen geben an, durch wie viele waagerecht, senkrecht und diagonal benachbarte Felder der Rundweg geht. - Kerzen (Philipp)
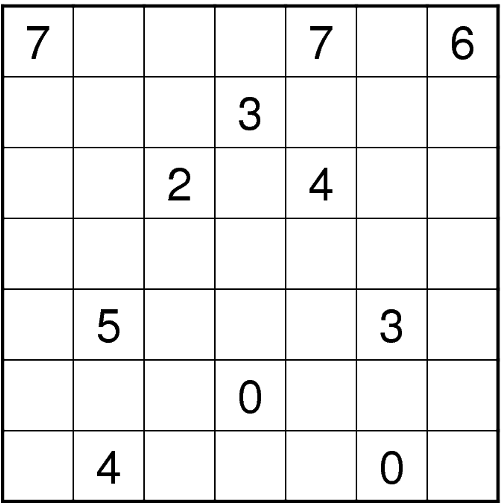
Tragen Sie in einige Felder Zahlen von 0 bis 4 so ein, dass jede vorgegeben Zahl die Summe der Zahlen in den benachbarten Feldern (auch diagonal) und jede eingetragene Zahl genau 4 minus die Anzahl der waagerecht und senkrecht benachbarten eingetragenen Zahlen ist. - Sudoku (Maria)
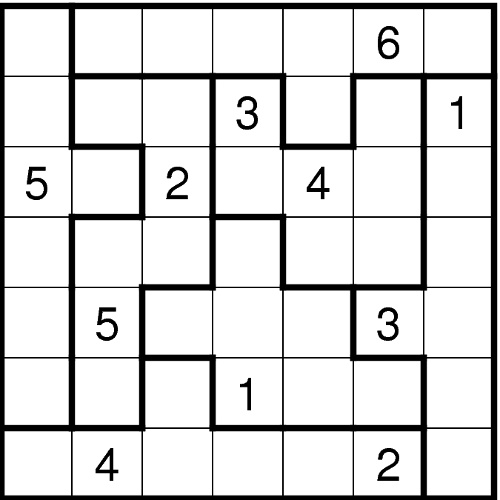
Tragen Sie die Ziffern von 1 bis 7 so in das Diagramm ein, dass in jeder Zeile, jeder Spalte und jedem fett umrandeten Gebiet jede Ziffer genau einmal vorkommt. - Tetromino-Minesweeper (Uvo)
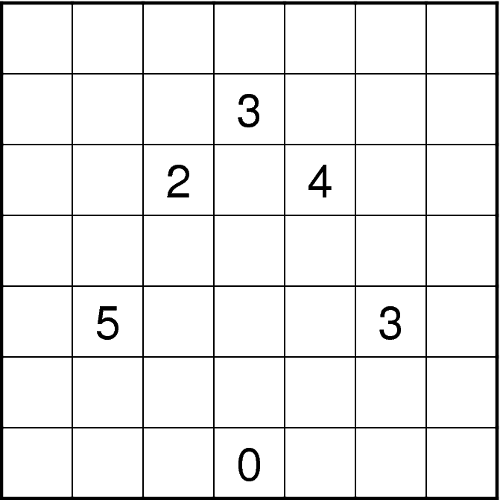
Die fünf Tetrominos sind im Gitter derart zu platzieren, dass sie einander nicht berühren, auch nicht diagonal. Die Tetrominos dürfen beliebig gedreht und gespiegelt werden. Die Zahlenfelder dürfen nicht von Tetrominos bedeckt werden; jede Zahl gibt an, wie viele der Nachbarfelder (horizontal, vertikal und diagonal) ein Tetromino-Segment enthalten. - Nanro (Philipp)
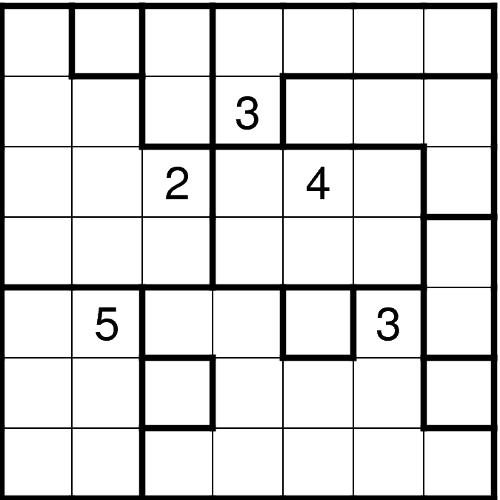
Schreiben Sie in einige der Felder Zahlen, so dass alle Zahlen innerhalb eines Gebiets gleich sind und die Anzahl der Zahlen in diesem Gebiet angeben. In jedem Gebiet muss mindestens eine Zahl stehen. Über Gebietsgrenzen hinweg dürfen sich Felder mit gleichen Zahlen waagerecht und senkrecht nicht berühren. Zudem darf kein 2x2-Bereich vollständig mit Zahlenfeldern bedeckt sein und alle Zahlenfelder müssen waagerecht und senkrecht zusammenhängen. - Höhle (Gabi)
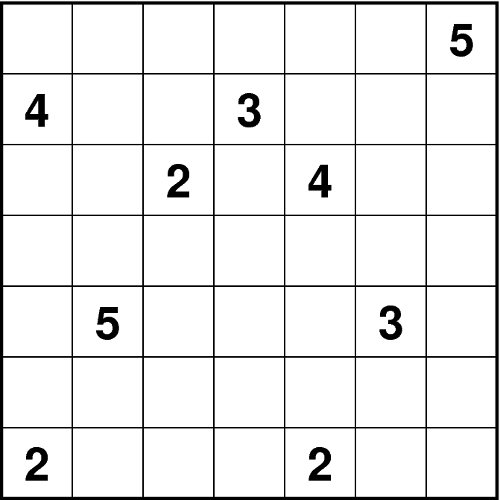
Färben Sie im Diagramm einige Felder schwarz, so dass ein Höhlensystem entsteht, welches die folgenden Eigenschaften haben soll: Alle Felder der Höhle (die weißen Felder einschließlich der Zahlenfelder) hängen zusammen. Alle Wände (die schwarzen Felder) sind mit dem äußeren Rand des Diagramms verbunden, d.h. es gibt keine Wandmasse, die komplett von weißen Feldern eingeschlossen ist. Zahlenfelder dürfen nicht geschwärzt werden. Jede Zahl gibt an, wie viele Felder der Höhle man von dem entsprechenden Feld aus in waagerechter oder senkrechter Linie sehen kann, in alle möglichen Richtungen aufsummiert; das Zahlenfeld selbst wird hierbei mitgezählt. - Doppelblock (Jürgen)
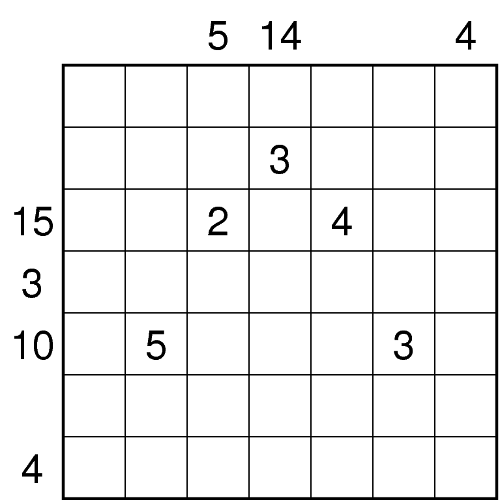
Schwärzen Sie einige Felder und tragen Sie die Zahlen von 1 bis 3 in die verbleibenden Felder so ein, dass in jeder Zeile und jeder Spalte genau zwei Felder geschwärzt sind und jede Zahl genau einmal vorkommt. Die Zahlen am Rand geben dabei die Summe der Zahlen an, die sich zwischen den beiden Schwarzfeldern befinden. - Multi-Sikaku (Helena)
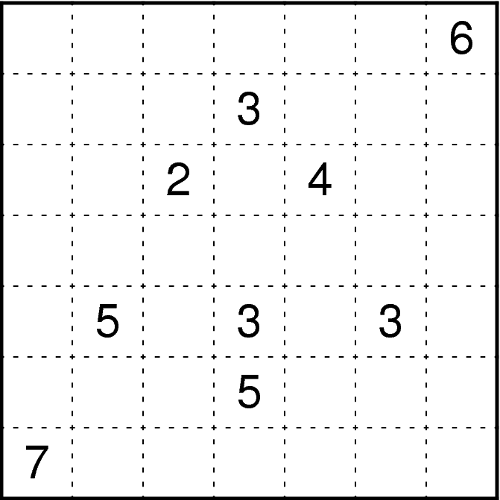
Unterteilen Sie das Diagramm entlang der Gitterlinien in rechteckige Gebiete, so dass jedes Gebiet genau eine Zahl enthält. Die Anzahl der Felder des Gebiets muss ein Vielfaches der Zahl sein, die sich in dem Gebiet befindet.Im Nachhinein stellte sich das Rätsel als mehrlösig heraus. Das ist der Jury aber nicht aufgefallen.
- Knapp-daneben Eckenrundweg (Nicole)

Zeichnen Sie entlang der gepunkteten Linien einen geschlossenen Weg ein, wobei nicht alle Gitterpunkte durchlaufen werden müssen. Die Zahlen in den Feldern geben an, wie viele der benachbarten Ecken für den Weg verwendet werden. Der Weg darf sich nicht selbst kreuzen oder berühren. Achtung: Alle Zahlen sind knapp daneben, das heißt, sie sind entweder um eins größer oder um eins kleiner als die Zahl, die in dem Feld tatsächlich stehen sollte. - Sudoku (Peggy)
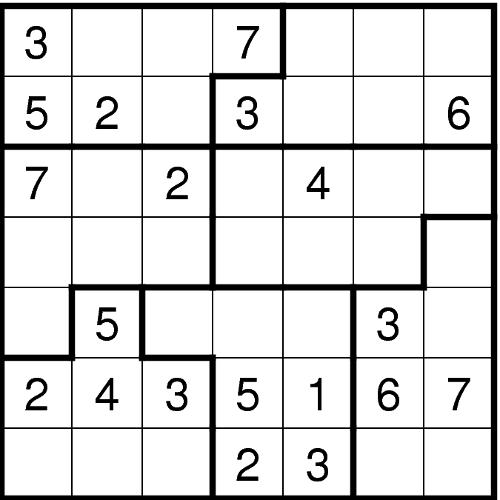
Tragen Sie die Ziffern von 1 bis 7 so in das Diagramm ein, dass in jeder Zeile, jeder Spalte und jedem fett umrandeten Gebiet jede Ziffer genau einmal vorkommt. - Hitori (Dandelo)

Schwärzen Sie einige Felder im Diagramm so, dass in den verbleibenden Feldern jede Zahl in jeder Zeile und jeder Spalte nur maximal einmal vorkommt. Alle ungeschwärzten Felder müssen miteinander verbunden sein (das heißt, die Schwarzfelder dürfen das Rätsel nicht in zwei Teile teilen). Zudem dürfen keine zwei Schwarzfelder benachbart sein.Das Rätsel wurde erst nach dem offiziellen Ende der Bearbeitungszeit abgegeben und deswegen nicht gewertet.
