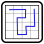
Stationary Loop Deconstruction (1-7)
(Eingestellt am 18. Februar 2025, 08:00 Uhr von Playmaker6174)
Here's a project with an idea that has also been in my shimmering list of puzzle ideas for a long while, though it's more like an alternative route of that idea.
This is also my first step into the deconstruction concept and stations concept, at the end it rather acts like a proof of concept and it's built on a smaller size of the main thing with digits 1-9 (which I haven't tried so yet), but if this one gets enough appreciation then I may try to set the main thing at some point in the future.
For now, let's see how this goes:
Rules:
- Located within the grid are 7 orthogonally connected regions that contain digits 1-7 once each so that digits don't repeat in any row or column of the entire grid. Any two regions cannot touch orthogonally but may touch diagonally.
- The 'region number N' of a region is defined as digit N in the top-left cell of that region, i.e. the left most cell in the top most row (in this case, top most is prioritized over left most). Each digit from 1 to 7 must occupy a region number once.
- Draw a single loop, which goes orthogonally and doesn't branch or intersect itself, that must go through all of the non-digit cells AND ALSO must visit each region once at ONLY the respective region number cell, which follows in the increasing order before back to 1 again (i.e. 1 -> 2 -> ... -> 7 -> 1).
Whenever the loop goes through a region number cell, it must make a 90 degrees turn at that cell.
- A cell with arrow[s] in it contains digit that's equal to the combined amount of cell borders that the loop goes through in the indicated direction[s], including the borders of arrow cells as well if available.
- Every given empty cell doesn't contain digit or loop segment at all.
An example of how the rules work can be found below. It's not an actual puzzle, but rather acts as an illustration for how the main concept works and also how the arrow rule works.
Puzzle: Penpa plus - Sudokupad
The answer check in penpa link will activate once all of the digits are correctly filled and also the loop is correctly drawn. For now, good luck and have fun solving!
Lösungscode: Enter column 9 (the marked column) from top to bottom: For a digit cell, enter the digit only; while for a non-digit cell, enter capital letter L if it's a loop's turn or capital letter I if it's a loop's straight segment.
For example, column 1 in the example image would be: LIL3L42.
Kommentare
am 27. Februar 2025, 03:11 Uhr von tallcat
Very much enjoyed testing this!! Looking forward to the main event/main course.
am 24. Februar 2025, 05:16 Uhr von peacherwu2
All worked out beautiful! True gem!
am 24. Februar 2025, 00:30 Uhr von wildbush7
Fantastic puzzle, had a great time solving it!
am 21. Februar 2025, 22:26 Uhr von Jesper
Great puzzle, thanks!
am 20. Februar 2025, 19:58 Uhr von ONeill
Really cool puzzle, thanks :)
am 18. Februar 2025, 19:06 Uhr von Christounet
Yeah, #2 please. Thanks :)
am 18. Februar 2025, 18:44 Uhr von TripleABattery
Really nice puzzle, thank you! I, for one, would love to see a 1-9 version :)
am 18. Februar 2025, 15:23 Uhr von Piatato
Awesome puzzle! Very cool ruleset, I hope that big version is gonna work out as well!