Shade Your Own Puzzle: Fillomino vs Cave ft. Parity #3 - N difference (13x13)
(Eingestellt am 4. Januar 2025, 03:30 Uhr von Playmaker6174)
To start off the new year, here's something rather unexpected...
The following puzzle actually started out as an entry for a "slow setting" competition that's held on CTC Discord server by Gene few days ago. Each of us as competitors was given only 24 hours and required to set a puzzle based on an interesting particular concept that had been done before over here by DubiousMobius on several occasions.
It was interesting and also cheerful to hear at the end that my entry got the second place overall despite being the only pencil puzzle entry, all of that thanks to the never-ending efforts I got to refine and finish the final portions of this entry (and with some frustration mixed in the middle of the setting, of course).
Regardless, thanks to Gene, DubiousMobius and other people who helped and also joined in the competition for providing such a fun and sweet experience before the new year came!
Anyway, I think this might be one of the most harmonized puzzles I've ever made in terms of layers of logic, let's see how this appears to everyone else:
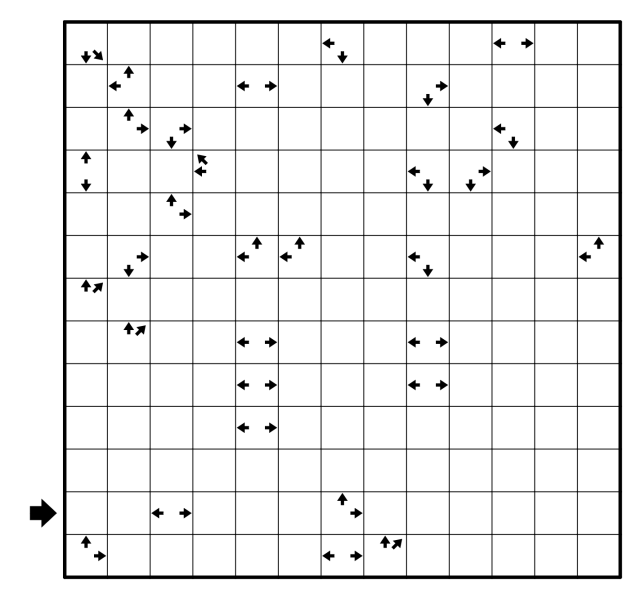Rules:
- Shade some cells in the entire grid so that all of the unshaded cells together form an orthogonally connected area, while each group of the shaded cells has to connect to the grid's perimeter.
- In addition, divide the entire grid into smaller regions and enter into each cell a number that's equal to the size of its region (i.e the number of cells in its region). No two regions of the same size can touch each other orthogonally (i.e sharing an edge).
- In the finished solution, every region must be either entirely shaded or entirely unshaded, and the sizes of all of the shaded regions must share the same odd/even parity while the sizes of all of the unshaded regions must share the other odd/even parity. Which parity belongs to which type of shading needs to be deduced.
- A number N in a cell containing a pair of two arrows means that two cells that are N cells away from that arrows' cell in the indicated directions must have the difference of N. (The case of two adjacent cells is counted as one cell away from each other)
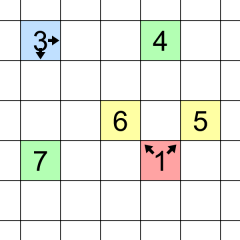
A few examples to clarify how the last rule works:
Puzzle: Penpa plus - Sudokupad
Good luck and have fun solving!
The following puzzle actually started out as an entry for a "slow setting" competition that's held on CTC Discord server by Gene few days ago. Each of us as competitors was given only 24 hours and required to set a puzzle based on an interesting particular concept that had been done before over here by DubiousMobius on several occasions.
It was interesting and also cheerful to hear at the end that my entry got the second place overall despite being the only pencil puzzle entry, all of that thanks to the never-ending efforts I got to refine and finish the final portions of this entry (and with some frustration mixed in the middle of the setting, of course).
Regardless, thanks to Gene, DubiousMobius and other people who helped and also joined in the competition for providing such a fun and sweet experience before the new year came!
Anyway, I think this might be one of the most harmonized puzzles I've ever made in terms of layers of logic, let's see how this appears to everyone else:
- Shade some cells in the entire grid so that all of the unshaded cells together form an orthogonally connected area, while each group of the shaded cells has to connect to the grid's perimeter.
- In addition, divide the entire grid into smaller regions and enter into each cell a number that's equal to the size of its region (i.e the number of cells in its region). No two regions of the same size can touch each other orthogonally (i.e sharing an edge).
- In the finished solution, every region must be either entirely shaded or entirely unshaded, and the sizes of all of the shaded regions must share the same odd/even parity while the sizes of all of the unshaded regions must share the other odd/even parity. Which parity belongs to which type of shading needs to be deduced.
- A number N in a cell containing a pair of two arrows means that two cells that are N cells away from that arrows' cell in the indicated directions must have the difference of N. (The case of two adjacent cells is counted as one cell away from each other)
A few examples to clarify how the last rule works:
Puzzle: Penpa plus - Sudokupad
Good luck and have fun solving!
Lösungscode: Enter row 12 (the marked row) from left to right, write letter S for each shaded cell and corresponding number for each unshaded cell
Gelöst von Tom-dz, Las4one, tuturitu, chien2000gl, nuzzopa, Tilberg, han233ing, zhangjinyang, itweb, Chefofdeath, krytolandros, SeveNateNine, GTLSE, Silverstep, Christounet, jaime, XIAOYING, Jesper, peacherwu2, Agent, sth, BloodbuzzCorio, ns08, ONeill, jkuo7, dogfarts, twobear, MazzleFlush, Lyun Licuss, Dragonslayer, LeiZ123321, Mr_tn
Kommentare
am 11. Januar 2025, 22:20 Uhr von Agent
Awesome puzzle, very smooth and with a nice variety of logic! Thanks for reminding me that Fillomino is such a great genre :)
am 9. Januar 2025, 10:44 Uhr von Jesper
Great puzzle, enjoyed it a lot, thanks!
am 8. Januar 2025, 22:55 Uhr von Christounet
Very pleasant and flowy puzzle. Felton much less difficult than its current 5* rating. Enjoying this serie ! Thanks :)
am 5. Januar 2025, 22:50 Uhr von krytolandros
Loved this!
am 4. Januar 2025, 17:26 Uhr von Tilberg
Very nice, a lot of fun. Thank you!
