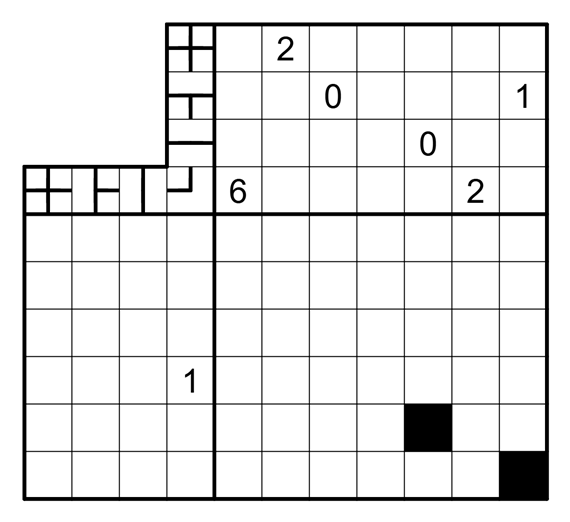
U-Bahn LITSO (6x7)
(Eingestellt am 27. Dezember 2024, 18:01 Uhr von the_cogito)
This is the second to last installment in this series of puzzles. I'll publish something smaller (and easier) still shortly. Enjoy!
Rules:
Solve on Penpa (Includes answer check for the loop only)
Solve on Sudokupad (No answer check)
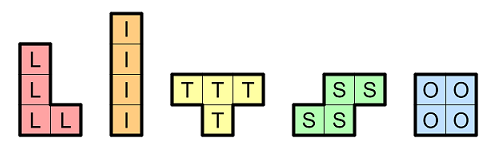
The five standard tetrominoes, ignoring rotation and reflections:
Rules:
- Draw a totally connected loop network through the centers of some cells, which may branch or turn, but may not have any dead ends. A clue outside the grid indicates how many times the corresponding line shape (i.e. a cross, branch, straight line, or turn) appears in the corresponding row or column, irrespective of the line shape's rotation.
- Divide the grid into non-overlapping tetrominoes such that every non-black cell is part of a tetromino. Orthogonally adjacent tetrominoes may not be the same shape, regardless of rotation or reflection.
- The loop network must cross the perimeter of every tetromino exactly 3 times. The loop network may pass freely through black cells.
Solve on Sudokupad (No answer check)
The five standard tetrominoes, ignoring rotation and reflections:
Lösungscode: From left to right, for every column except the last, the number of loop segments extending right from that column.
Zuletzt geändert am 28. Dezember 2024, 15:51 Uhr
Gelöst von dumediat, ONeill, jessica6, Zzzyxas, Piatato, Paletron, Mr_tn, misko, Jesper, jkuo7, tuturitu, filuta
Kommentare
am 9. Januar 2025, 18:10 Uhr von Jesper
Very nice, thanks!
am 30. Dezember 2024, 02:14 Uhr von Piatato
Lovely!
Zuletzt geändert am 28. Dezember 2024, 15:50 Uhr
am 28. Dezember 2024, 15:41 Uhr von jessica6
you mean, for every column except the *last*
------
Yes, thanks! My bad haha
