Logic Masters Deutschland e.V.

You've kept your old holiday string lights up for 27 years, but now your luck has run out and at least one bulb has become faulty. Every bulb from the faulty one on have gone out as well! The working bulbs are sharing too much voltage now and risk burning out!

---

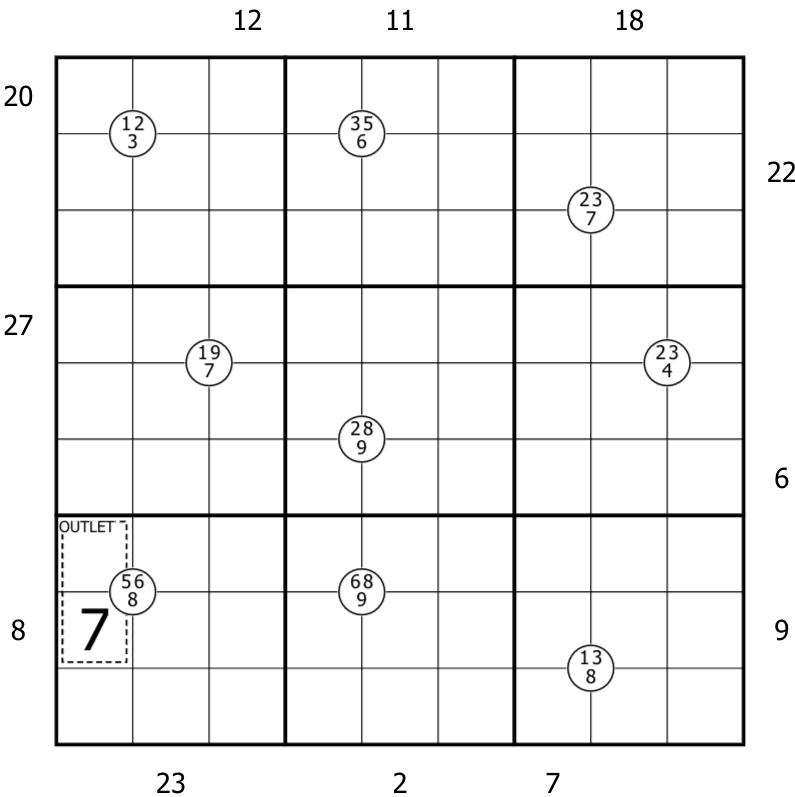
Find the orthogonal path (bulbs and wire) of the string lights from the outlet cage and determine at which point the bulbs are no longer lit. The path may not cross or branch.

Bulb cells: Each row, column and 3x3 region contains one bulb, each bulb having a distinct digit from the set 1-9. At least half of the bulbs are lit (whew!) and at least one bulb on the string is broken.

Wire cells: There are 3 orthogonally adjacent cells of wire between each set of two bulbs, to which they will connect orthogonally. Wire-cells have values [5-9] until the first burnt out bulb, and within the burnt out section they hold values [1-5].
The wire cells may not completely fill a 2x2 area (bulb cells are not wire cells)

Outlet cells: The first bulb is orthogonally adjacent to the outlet, shares its region and is working. The product of the cells in the outlet determines the voltage the lit bulbs must handle; the sum of lit bulbs must equal this value.

Meter clues: Clues outside the box represent the sum of all digits on wire cells until the first bulb is seen in the clue's row or column.

Quadruples: Every digit in a circle has to be assigned to one vof the surrounding cells.

---

Play on SudokuPad