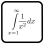Logic Masters Deutschland e.V.

This is part of an Exam question for the course "MATH4141: Number Theory and Applications" at HKUST. Some knowledge of elementary number theory is required to solve this puzzle.


Fill in the 4 × 4 grid with four distinct digits from {0, 1, 2, 3, 4, 5, 6, 7, 8} such that

• Each row, column, and L-shaped region does not contain repeated digits.
• The digits are all quadratic residues (mod 17).
• The 4-digit integer formed by the first row is a perfect square.
• Each clue outside the grid shows the number of ways the 4-digit integer in that column/row can be expressed as a sum of two squares of nonnegative integers (up to permutation).

Note: If a “4-digit integer” starts with a zero, we consider it a 3-digit integer instead. (e.g. “0123” is treated as 123.)