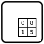
123 magic
(Eingestellt am 16. August 2024, 17:22 Uhr von fractalminding)
Lösungscode: Row 1
Kommentare
am 1. September 2024, 09:44 Uhr von michael_787
For all those who were experimenting: There is only one way to fill one of the boxes (I don't want to give away which box). Complete this box, and the rest is pretty much auto-fill due to the non-consecutive constraint.
am 28. August 2024, 00:16 Uhr von Joely
enjoyed this little speed run. nice puzzle :)
am 28. August 2024, 00:11 Uhr von Joely
Macintux, there is a constraint about a third of the way through where you can deduce two digits to not be a pencil marked pair as they are consecutive with one another. It will then allow you to place the digits. Hope this helps :)
am 18. August 2024, 19:25 Uhr von macintux
@brandon_bot Thanks, that’s more or less what I did, with less penciling. After identifying all of the first-order negative constraints, I decided to drop a digit in R6C5 and see what happened.
Fortunately it worked out.
am 18. August 2024, 11:11 Uhr von macintux
I solved it, but purely by luck: I started with one digit that would impose enough constraints that I could proceed to completion.
I’d love to know how this could be solved without experimenting by placing a digit.
am 17. August 2024, 12:27 Uhr von permafrostyx
yay
am 16. August 2024, 19:32 Uhr von PinkNickels
Fun speed run. 2:00 today.