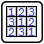
Augur's gift (Japanese sums/Mean mini/Kropki)
(Eingestellt am 24. Mai 2024, 03:09 Uhr von dumediat)
From March to May 2024, I hosted a bracket tournament akin to "March Madness" in the United States, where participants selected a constraint for each round to use against their opponent. For the semifinals, I held a mini contest where people could try to predict the four constraints to be used for the round, with the prize being a 6x6 puzzle created by me. The winner of this was chameleon, who chose Japanese sums with Kropki as their constraint choices for their prize puzzle. I may have gotten a little carried away with the concept of a "6x6" puzzle, but they enjoyed it enough where they suggested I publish it here for you all to enjoy as well!
Ratings, comments, and feedback are much appreciated! Please feel free to reach out to me on Discord if you have any comments or questions. Please also feel free to try my other puzzles here.
Rules:
- Place the digits 1 to 9 in the 3x3 grid and the 6x6 grid (the white cells) such that no digit repeats in any row or column. The 3x3 grid contains a set of three digits from 1 to 9 (to be determined by the solver), and the 6x6 grid contains the remaining set of six digits. For example, if the 3x3 set is {247}, then the 6x6 set must be {135689}.
- Shade some cells in the 6x6 grid and fill all blue cells with positive integers. Numbers in blue cells indicate the sums of contiguous segments of unshaded cells in that row or column of the 6x6 grid, in the correct order. There must be at least one shaded cell separating two segments.
- Numbers with a white dot between them must be consecutive, and numbers with a black dot between them must be in a 1:2 ratio. If there is no dot between two numbers that are both in blue cells, neither of these characteristics can be true.
- In the final solution, all cells will contain a number.
Links:
Penpa+: https://tinyurl.com/2bbj5g8z
SudokuPad: https://sudokupad.app/p3nkr0w7we?setting-conflictchecker=0
Note: The SudokuPad solution check will trigger once all single digit numbers are correctly entered, whereas the Penpa+ solution check will only trigger once all numbers and shading are correctly placed.
Lösungscode: Considering the top-left cell of the white 3x3 grid as row 1 column 1: Column 9 from top-to-bottom (nine numbers)
Kommentare
am 21. Juni 2024, 19:18 Uhr von Bankey
That was super fun. Thanks, @ dumediat :).
am 3. Juni 2024, 22:19 Uhr von Christounet
Awesome idea, love the mean minis, especially with multigrids ! Thanks :)
am 28. Mai 2024, 18:18 Uhr von wisty
Every step was super clean! Enjoying the dumediat jsum arc
am 25. Mai 2024, 15:17 Uhr von marcmees
very nice. thanks
am 24. Mai 2024, 16:45 Uhr von Jesper
Very nice, thanks!
am 24. Mai 2024, 15:12 Uhr von MicroStudy
verified banger alert
am 24. Mai 2024, 15:04 Uhr von ildiko
Genial.
am 24. Mai 2024, 14:17 Uhr von chameleon
Thank you very much for the gift! I loved it the very moment when I saw the dots in the JSS clues area :)
am 24. Mai 2024, 10:13 Uhr von Piatato
Very nice, inventive way to make a mean mini!
am 24. Mai 2024, 09:30 Uhr von Snookerfan
Great puzzle! Thank you
am 24. Mai 2024, 07:44 Uhr von zzw
Awesome puzzle! Really cool idea, and very well executed with lots of interesting steps.