Negative Lines Series #4 - Five Below (Negative Renban)
(Eingestellt am 12. April 2024, 15:46 Uhr von Mikemerin)
Part of the Negative Lines Series
Another minimal puzzle easier than the others in this series and a test to see how small of a grid this ruleset could work in, while also getting some practice to help with creating a 9x9 version.
As usual, resist any urges to bifurcate as there is logic at each step!
---
Latin Square: place 1-5 in each row and column.
Renban: for numbers 2-4, row N (horizontal) and column N (vertical) both have lines N long in the listed orientations. Lines have consecutive digits in any order, can overlap, and all lines are given.
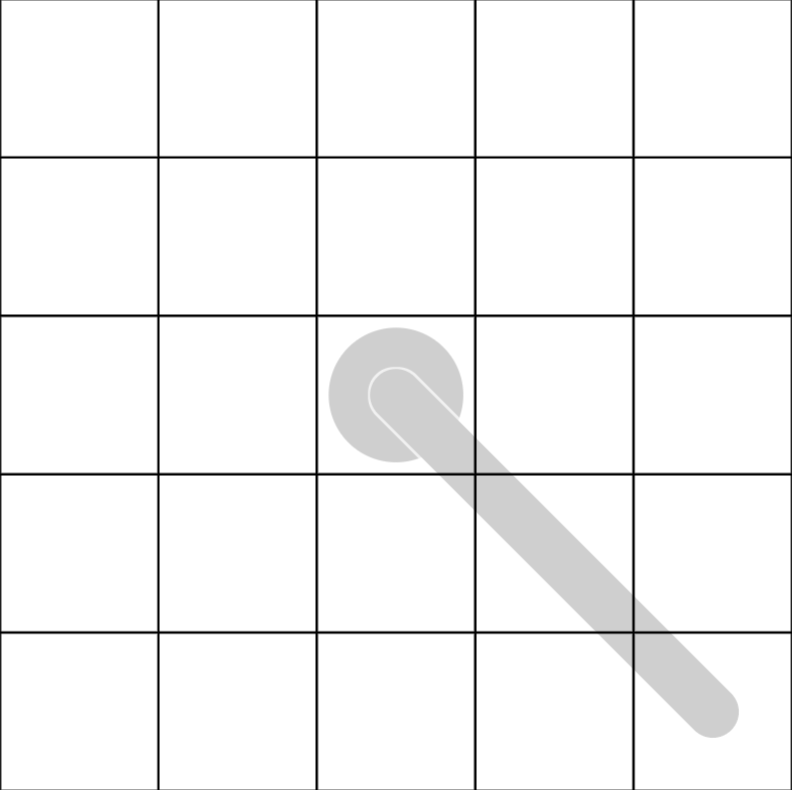
Thermometer: digits increase from the bulb.
---
Solve in Sudokupad (includes solution) or F-Puzzles
This ruleset is similar to a Kropki puzzle with a negative constraint, where if "all dots are given" and none are in the grid, adjacent cells cannot be consecutive or be in a 2:1 ratio. For a general hint regarding this ruleset: putting digits 1324 in R4C1-4 would break the puzzle as there is now a run of 4 consecutive digits in any order.
-----
Another minimal puzzle easier than the others in this series and a test to see how small of a grid this ruleset could work in, while also getting some practice to help with creating a 9x9 version.
As usual, resist any urges to bifurcate as there is logic at each step!
---
Latin Square: place 1-5 in each row and column.
Renban: for numbers 2-4, row N (horizontal) and column N (vertical) both have lines N long in the listed orientations. Lines have consecutive digits in any order, can overlap, and all lines are given.
Thermometer: digits increase from the bulb.
---
Solve in Sudokupad (includes solution) or F-Puzzles
This ruleset is similar to a Kropki puzzle with a negative constraint, where if "all dots are given" and none are in the grid, adjacent cells cannot be consecutive or be in a 2:1 ratio. For a general hint regarding this ruleset: putting digits 1324 in R4C1-4 would break the puzzle as there is now a run of 4 consecutive digits in any order.
-----
Lösungscode: Row 1 and Column 1 (10 digits)
Gelöst von SKORP17, Woody03130, zhangjinyang, PippoForte
Kommentare
Zuletzt geändert am 26. April 2024, 02:48 Uhr
am 25. April 2024, 22:40 Uhr von michael_787
Would love to try this puzzle, but I'm struggling to make sense of the Renban constraint. Is this even a correct English sentence?
—-
Hey fellow Mike, I have a more detailed explanation of the Renban rule in the other puzzles in the series along with example images, but basically for this puzzle as examples:
Row 2 has lines 2 long, and since no lines are present in the puzzle this means no adjacent cells in row 2 can be consecutive (similar to a negative white Kropki restraint). The same goes for column 2. Repeat for rows/columns 3 and 4 but with line lengths of 3 and 4 respectively.
Hope this helps!
-MM