Pirate Islands
(Eingestellt am 18. Juni 2023, 16:54 Uhr von Torvelo)
Platziere einige Inseln und zeichne einen Weg von jedem Schiff zu ein der Inseln.
Die Inseln funktionieren wie in Nurikabe. Inseln bestehen aus orthogonal zusammenhängende Felder und berühren einander nicht orthogonal. Jede Insel muss genau eine Ziffer haben, und jede Ziffer gehört zu einer Insel. Die Ziffer erzählt die Große der Insel. (Im Gegensatz zu Nurikabe, 2x2-Wassergebiete und nicht zusammenhängende Wassergebiete sind nicht verboten)
Aus jedem Handelsschiff (weiße Schiffe) muss ein Weg durch Wasserfelder zu einem Hafen (Felder mit Vorgabsziffern) gezeichnet werden, und zu jedem Hafen muss mindestens ein Schiff kommen. Die Wege der Schiffe laufen waagerecht und senkrecht durch die Mittelpunkte von Felder. Die Wege dürfen einander oder sich selbst nicht schneiden oder berühren. Jedes Wasserfeld, die die Piraten (schwarze Schiffe) nicht sehen, muss genau einmal besucht werden. Die Piraten sehen in orthogonal Richtungen unbeschränkt entfernt, aber sie können nicht durch Inseln sehen. Piraten dürfen die Handelsschiffe nicht sehen.
Im Gewittersturmfelder müssen die Schiffe geradeaus gehen, und im Wirbelsturmfelder dürfen sie nicht geradeaus gehen.
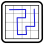
Zwei kleine Beispiele:
Das Rätsel:
Lösungscode: Zeilenweis von oben nach unten, gebe die Anzahl der Felder, wo ein weg abbiegt. (im ersten Beispiel wäre der Code 333200)