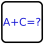Logic Masters Deutschland e.V.

Es gelten die üblichen Chaos-Construction-Regeln. Jede Reihe, Spalte, und fett umrandete Region enthält je einmal die Ziffern 1 bis 9. Jedoch müssen die Regionen vom Löser erkundet werden. Ein Bruchstück einer Regionsgrenze ist bereits vorgegeben.

Hinweise ausserhalb des Gitters sind zugleich Border-Sum- und Parity-Party-Hinweise.

Erstens deuten sie die Summe der Ziffern an, die über die erstgesehene Regionengrenze hinweg nebeneinander liegen, UND

zweitens deuten sie die Summe der Ziffern an, die von diesem Blickpunkt aus angetroffen werden... entweder bis zur ersten geraden ODER bis zur ersten ungeraden Ziffer. Sieht man zum Beispiel eine 15 am unteren Ende einer Spalte, dann könnte diese Spalte, von unten nach oben lesend, u.a. 7-8, 8-7, 1-3-5-6, oder auch 2-6-4-3 enthalten. Es könnte aber nicht 1-2-3-4-5 oder 2-6-3-4 sein.. die letzte Ziffer muss in ihrer Parität (engl: Parity) von den vorhergehenden abweichen. Note: Wenn die Randzahl kleiner als 10 ist, dann könnte einfach die erste Ziffer angegeben sein (Sprich: die Summe von null geraden und einer ungeraden Zahl, bzw. umgekehrt!)

Ein '?' kann für jede beliebige einzelne Ganzzahl einstehen. Über der 4. Spalte steht ebenfalls eine beliebige Ganzzahl weniger als 14.

Penpa-Fassung

Im CtC-App