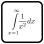Cylic Modular Casscade

(Eingestellt am 22. September 2022, 09:06 Uhr von glenfletcher)

Hinweis: Übersetzt aus dem Englischen mit Google Translate

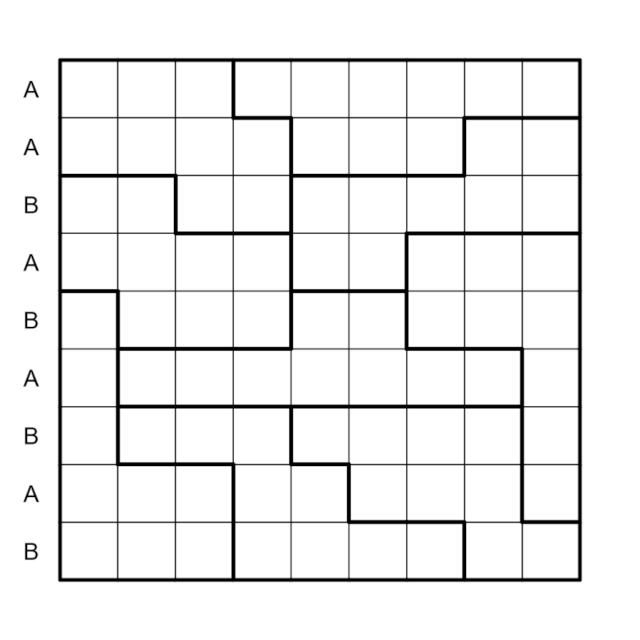
Sofern nicht ausdrücklich angegeben, gelten die Regeln für das Toroidgitter, das gebildet wird, indem das bereitgestellte Gitter horizontal und vertikal umwickelt wird.
Ziffern dürfen sich in einer Region nicht wiederholen.
Ziffern müssen in jeder Zeile denselben 9er-Zyklus bilden.
Für jede 4er-lange Unterfolge des 9er-Zyklus über jede Zeile hinweg muss die Summe der ersten und letzten Ziffer modulo 9 mit der Summe der mittleren zwei Ziffern kongruent sein. (d.h. R1C9 + R1C3 ≡ R1C1 + R1C2 (mod 9)).
Die Summe der Vorwärtsdifferenzen Modulo 9 zwischen allen eindeutigen Paaren im 9-Zyklus über jede Zeile muss minimiert werden, vorbehaltlich der anderen Regeln. (d. h. (R1C1 – R1C9 (mod 9)) + (R1C2 – R1C1 (mod 9)) + … + (R1C9 – R1C8 (mod 9)) muss minimiert werden).
Ziffern müssen in jeder Spalte denselben 9er-Zyklus bilden.
Ziffern müssen auf jeder positiven Diagonale denselben 9er-Zyklus bilden.
Ziffern dürfen Modulo 3 nicht kongruent sein mit Ziffern, die orthogonal benachbart oder entlang einer positiven Diagonale benachbart sind. (d.h. die folgenden müssen alle falsch sein, R3C4 ≡ R2C4 (mod 3), R3C4 ≡ R4C4 (mod 3), R3C4 ≡ R3C3 (mod 3), R3C4 ≡ R3C5 (mod 3), R3C4 ≡ R2C5 (mod 3) und R3C4 ≡ R4C3 (mod 3)).
Ziffern müssen einen wiederkehrenden 3-Zyklus bilden, der aus den Ziffern besteht, die Modulo 3 entlang negativer Diagonalen kongruent sind, und der Zyklus muss derselbe Zyklus für jede Gruppe von Ziffern sein, die Modulo 3 kongruent sind. (d. h. R1C4 ≡ R2C5 ≡ R3C6 (mod 3) aber R1C4 ≠ R2C5 ≠ R3C6 ≠ R4C7 = R1C4).
Die am Rand des Rasters angezeigten Werte (A und B) sind die Summe der Ziffern zwischen (1 und 9) im bereitgestellten Raster und haben eine Differenz von 5.