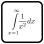3D Color (Original Sudoku Variant)
(Eingestellt am 3. September 2022, 13:22 Uhr von DarkOrange224)
Dies ist das erste Puzzle, das ich erstellt und ein bisschen ungewöhnlich (bitte entschuldigen Sie die etwas umfangreiche Regelbeschreibung), aber nach einiger anfänglicher Visualisierung sollte es eine ziemlich glatte Lösung sein, die viele bekannte Logik enthält.
Klicken Sie hier, um dies auf F-Puzzles zu lösen
⬤--〇--⬤--〇--⬤--〇--⬤--〇--⬤--〇--⬤--〇--⬤--〇--⬤--〇--⬤--〇
Regeln:
Es gelten normale Sudoku-Regeln.
Jede Ziffer im Raster wird durch bis zu drei Farben zusammen definiert. Eine Ziffer kann blau (gerade) oder orange (ungerad), rot (höher als fünf), grün (unter fünf) oder weder (fünf genau) und lila (eine perfekte Quadrat- oder Würfelzahl) oder gelb (andere / 'unvollkommen') sein. Wenn beispielsweise eine Zelle als blau, grün und gelb gefunden wird, muss sie zwangsläufig die einzige gleichmäßige, niedrige und unvollkommene Zahl, zwei enthalten.
Ein farbiger Punkt in der Ecke von vier Zellen zeigt eine Überwältigung in diesen Zellen (d.h. es gibt mehr von dieser Farbe als das Gegenteil). Beachten Sie, dass eine Überwältigung so wenig wie zwei rote oder grüne Zellen sein kann, wenn der vierte auch eine fünf oder so viele wie alle vier Zellen derselben Farbe enthält. Es sind nicht alle möglichen Punkte gegeben.
Lösungscode: Zeile 7
Kommentare
am 5. September 2022, 15:11 Uhr von britboy3456
Really loved this puzzle, but I do really agree that it is much more enjoyable to solve it on CTC than f-puzzles because of colouring a cell with multiple colours.
am 4. September 2022, 05:57 Uhr von AstralSky
Thanks! By the way, the CTC web app supports a cell be colored with more than one color. Maybe you can include a CTC link for puzzles like these.
am 4. September 2022, 03:25 Uhr von DarkOrange224
Yay - glad that you enjoyed it! =]
@AstralSky - I see that you found the answer already, but for any with similar first thoughts, some more clarification:
(WARNING, SLIGHT SPOILERS AHEAD)
Each cell actually has multiple colors at once. This may be hard to show on some software, but when I test it I just use color for the first dimension solved, then numbers (the remaining possibilities) for the other passes. So, yes, a red dot can definitely have four purple around it (in one dimension), and also maybe three red (in another dimension) and also maybe three blue (in the final dimension). This would mean that at least two of the numbers are the same, namely eight (purple for perfect, red for high, blue for even), and therefore they would have to be diagonally offset... I hope that this helps someone to enjoy the puzzle more.
am 4. September 2022, 02:45 Uhr von DarkOrange224
Updated German.
Thanks, @Raumplaner!
am 3. September 2022, 17:08 Uhr von AstralSky
Very fun and creative puzzle!
am 3. September 2022, 14:41 Uhr von Leonard Hal
A nice puzzle. I'm looking forward to more of your puzzles
am 3. September 2022, 13:34 Uhr von AstralSky
Question.Does the preponderance just apply to a pair of colors, or to all other colors?(example:if it is possible to have 4 purple cells around a red dot?)