μ-Dots and Totient Sandwiches
(Eingestellt am 16. Juni 2022, 20:22 Uhr von Hrafnsvaengr)
What started out as a very silly idea turned into this, a very niche but fun little puzzle based on two functions from number theory. It shouldn't be too difficult, although the rules may seem more complicated at first than they actually are.
A link for the puzzle on f-puzzles can be found here and on CtC here.
Alternatively, the rules can be simplified as so, if you are familiar with the Möbius function, μ(n), and the Euler totient function, φ(n).
A link for the puzzle on f-puzzles can be found here and on CtC here.
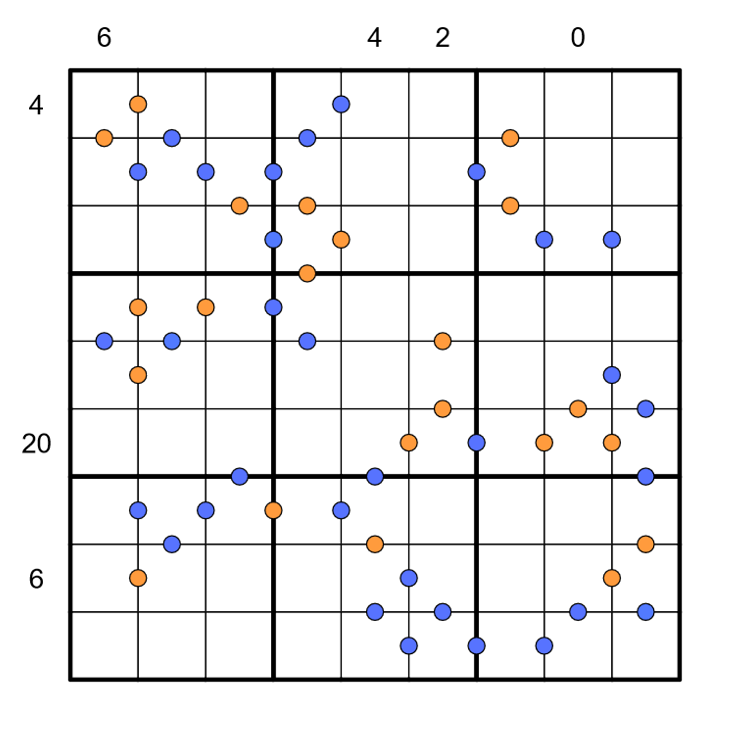
- Normal sudoku rules apply.
- If the product of two orthogonally adjacent digits is the product of an even number of distinct primes, there is a blue dot between them.
- If the product of two orthogonally adjacent digits is the product of an odd number of distinct primes, there is an orange dot between them.
- If the product of two orthogonally adjacent digits is the product of a perfect square (other than 1) and any other number, there is no dot between them.
- The clues around the edge of the grid are totient sandwiches.
- Let N be the sum of the digits that appear between the 1 and 9 in a given row or column.
- The clue adjacent to that row or column is equal to the number of positive integers, up to N, which share no factors with N.
μ-Dots:
Totient Sandwiches:
Alternatively, the rules can be simplified as so, if you are familiar with the Möbius function, μ(n), and the Euler totient function, φ(n).
- Normal sudoku rules apply.
- Let a,b be two orthogonally adjacent cells. If there is a blue dot between them, μ(ab)=1; if there is an orange dot between them, μ(ab)=-1; if there is no dot, μ(ab)=0.
- Let si be the digits appearing between the 1 and 9 in a row or column. A clue outside the grid is equal to φ(Σ si) in the corresponding row or column.
Lösungscode: Row 4 and then column 3, without commas or spaces.
Zuletzt geändert am 16. Juni 2022, 20:23 Uhr
Gelöst von Arashdeep Singh, kublai, RJBlarmo, baris, SKORP17, Xean, Leonard Hal, KevinTheMH, hibye1217, Woody03130
Kommentare
am 17. Juni 2022, 00:54 Uhr von RJBlarmo
Fun puzzle, nothing too difficult once you really consider how the Mobius function works. Needed to have a totient function table up though :)
am 16. Juni 2022, 22:13 Uhr von kublai
WOW! Once I got the mu and totient constraints sorted it wasn't so bad, but that part was tricky enough to bump it up a little on difficulty.
am 16. Juni 2022, 21:23 Uhr von Arashdeep Singh
Nice puzzle. Learned the functions through it. Thanks :)
am 16. Juni 2022, 20:23 Uhr von Hrafnsvaengr
Typo correction



