Yajitatami / Yajisan-Kazusan doppelgänger
(Eingestellt am 25. November 2021, 13:31 Uhr von Aspartagcus)
I've been into setting doppelgänger puzzles lately, so I thought I'd share a couple more that I've made. :)
This puzzle is solvable both as a yajitatami and as a yajisan-kazusan.
The yajitatami is easier (which means I like the yajisan-kazusan better).
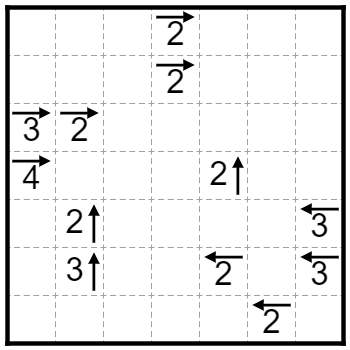
Yajitatami:
Divide the grid into 1xn regions, where n>1, such that the digit in a clued cell equals the amount of cells in that region as well as the amount of regions seen in the direction of its arrow. There must always be a border directly in front of an arrow, and nowhere in the grid may a cross be formed by borders (four border lines eminating from the same point).
Link to puzzle
Rules and example on puzz.link
Yajisan-kazusan rules: Shade some cells in the grid such that no two shaded cells are orthogonally adjacent and all the unshaded cells form a single connected region. If an unshaded cell has a clue in it, then that clue gives the number of shaded cells in the direction of the arrow. A clue in a shaded cell has no bearing on the puzzle and can be ignored.
Link to puzzle
Rules and example on puzz.link
Both puzzles (Penpa+)
Answer check on shading (Yajisan-Kazusan) and edges (Yajitatami) together.
Enjoy!
This puzzle is solvable both as a yajitatami and as a yajisan-kazusan.
The yajitatami is easier (which means I like the yajisan-kazusan better).
Yajitatami:
Divide the grid into 1xn regions, where n>1, such that the digit in a clued cell equals the amount of cells in that region as well as the amount of regions seen in the direction of its arrow. There must always be a border directly in front of an arrow, and nowhere in the grid may a cross be formed by borders (four border lines eminating from the same point).
Link to puzzle
Rules and example on puzz.link
Yajisan-kazusan rules: Shade some cells in the grid such that no two shaded cells are orthogonally adjacent and all the unshaded cells form a single connected region. If an unshaded cell has a clue in it, then that clue gives the number of shaded cells in the direction of the arrow. A clue in a shaded cell has no bearing on the puzzle and can be ignored.
Link to puzzle
Rules and example on puzz.link
Both puzzles (Penpa+)
Answer check on shading (Yajisan-Kazusan) and edges (Yajitatami) together.
Enjoy!
Lösungscode: The amount of regions in each row (from top to bottom) for the yajitatami, followed by the amount of shaded cells in each row (from top to bottom) for the yajisan-kazusan.
Gelöst von CastleSheepside, ymhsbmbesitwf, MagnusJosefsson, Mark Sweep, Dandelo, PixelPlucker, Vebby, Jesper, saskia-daniela, jkl, Nothere, godoffours, rimodech, CJK, sandmoppe, moeve, CHalb, bernhard, JTDUNX, jessica6, moss, Dugong, AnnaTh, starelev5, skywalker, zorant, misko, effervescentblizzard, ildiko, Uhu, BenceJoful, jkuo7, webato, Someguy77
Kommentare
am 17. Dezember 2021, 17:27 Uhr von jessica6
yaji... learning japanese with Logic Masters?




