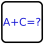Logic Masters Deutschland e.V.

f-puzzles Link

Parity Party XVI

Es gelten die üblichen Windoku-Regeln. In jeder Spalte, Reihe, in jedem 3x3-Kasten und 3x3-Käfig kommen also die Ziffern 1-9 je einmal vor.

Sonderregeln von Parity Party: Zahlen am Rand geben die Summe der Ziffern an, die von diesem Blickpunkt aus angetroffen werden... entweder bis zur ersten geraden ODER bis zur ersten ungeraden Ziffer. Sieht man zum Beispiel eine 15 am unteren Ende einer Spalte, dann könnte diese Spalte, von unten nach oben lesend, u.a. 7-8, 8-7, 1-3-5-6, oder auch 2-6-4-3 enthalten. Es könnte aber nicht 1-2-3-4-5 oder 2-6-3-4 sein.. die letzte Ziffer muss in ihrer Parität (engl: Parity) von den vorhergehenden abweichen.

Wenn die Randzahl kleiner als 10 ist, dann könnte einfach die erste Ziffer angegeben sein (Sprich: die Summe von null geraden und einer ungeraden Zahl, bzw. umgekehrt!)

Offene Kreise am äusseren Rand eines Käfigs bedeuten, daß die benachbarte Zelle ausserhalb des Käfigs ein gültiger Parity-Party Hinweis für die Ziffern im Käfig ist. Zum Beispiel schaut R5S7 über und unter sich und gibt den Parity-Party-Wert auf beiden Seiten wieder. Hier müssen die Hinweise naturgemäß von 2-3 Ziffern erfüllt werden. Nicht alle Kreise sind unbedingt gegeben.