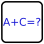The Power of Sudoku
(Eingestellt am 2. März 2021, 19:08 Uhr von 28degrees)
Whenever a caret (^) appears between two digits A and B, A^B appears directly after it. (Example: If a caret was between 3 and 4, then 3481 appears in that order, since 3^4=81) The equals signs are only to help show where A^B appears.
The digits on the marked diagonal sum to a perfect power.
Online link: https://f-puzzles.com/?id=yaxso4d5
For those that don't know, A^B means A multiplied by itself B times, so 3^4=3*3*3*3=81. A perfect power is a number of the form A^B, where B>1 (like a square, cube,...). These include 4,8,9,16,25,27,...
Lösungscode: Column 7
Kommentare
am 9. Juni 2021, 15:54 Uhr von Vebby
Very nice! Approachable and fun :)
am 8. Mai 2021, 02:54 Uhr von RockyRoer
I liked this a lot. Brainstorming a list of possible powers took a little time, but since there really aren't that many possibilities it was time well spent - and it lead to a pretty straight forward solve. Forgive me or make this hidden if you think it's too much of a spoiler - but as a math teacher, I'd hate to see people shy away from it because they think it's got difficult maths. It's quite approachable. Thanks for making it!
am 4. März 2021, 17:06 Uhr von henrypijames
I believe 1 is usually not considered a perfect power - in other words, not only B>1, but A>1 as well.
am 3. März 2021, 19:30 Uhr von 28degrees
Added definition of perfect power
am 3. März 2021, 19:19 Uhr von henrypijames
I agree: "perfect power" is not a term that everybody knows, especially if English is not their first language. If you've bothered to explain A^B, you should definitely explain perfect power.
am 2. März 2021, 23:55 Uhr von Gramor
Very nice puzzle