Mixed Doubles [Checkered Fillomino]
(Published on 15. January 2021, 01:30 by Panthera)
With an air of near-inevitability given how I got into setting these puzzles in the first place, I'm following up a Cracking The Cryptic-inspired Friendly Sudoku with a Cracking The Cryptic-inspired Checkered Fillomino. I suppose my next puzzle really ought to be inspired by one of Mark's solves, 'cause right now it's 2-0 to Simon... sorry, Mark! Turns out, I have no control over which concepts wind up tickling my fancy, so I can't promise anything. Oh, and I must also give credit to Jonas Gleim, whose formulation of the rules was to good not to borrow and then immediately ruin by making wordier...
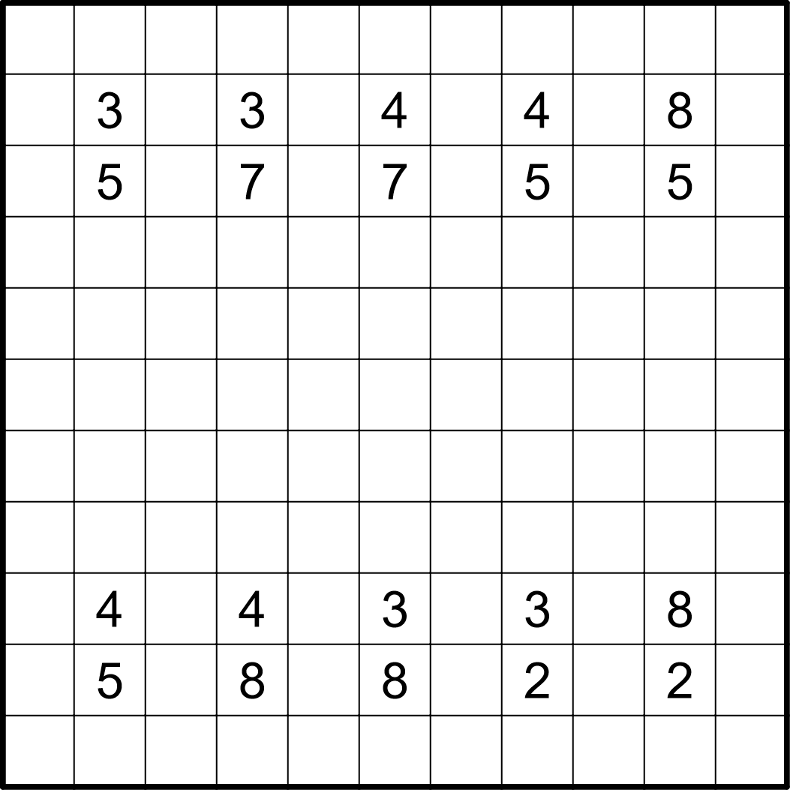
Rules
Normal fillomino rules apply: divide the grid into regions and place a number in each cell. The numbers within a region must all be the same and equal to the size of the region. Regions of equal size must not touch orthogonally, but may touch diagonally. A region may contain zero, one or more of the given numbers.
In addition, a "checkered" constraint applies: it must be possible to shade some regions fully such that two shaded regions or two unshaded regions never touch orthogonally. This is equivalent to saying that there are no T-junctions between regions, if that's how you'd rather think about it.
You can poke the puzzle on Penpa+ here, and as always, I wish you good luck and a (hopefully) enjoyable solve!
-~-~-~-~-~-~
Rules
Normal fillomino rules apply: divide the grid into regions and place a number in each cell. The numbers within a region must all be the same and equal to the size of the region. Regions of equal size must not touch orthogonally, but may touch diagonally. A region may contain zero, one or more of the given numbers.
In addition, a "checkered" constraint applies: it must be possible to shade some regions fully such that two shaded regions or two unshaded regions never touch orthogonally. This is equivalent to saying that there are no T-junctions between regions, if that's how you'd rather think about it.
You can poke the puzzle on Penpa+ here, and as always, I wish you good luck and a (hopefully) enjoyable solve!
Solution code: Row 5 and Row 7
Last changed on -
Solved by smckinley, Eggr, Jesper, jessica6, MagnusJosefsson, Lizzy01, ArchonE, harrison, NikolaZ, Dandelo, Alex, bernhard, wuzzle, Puzzle_Maestro, karen_birgitta, Mark Sweep, misko, Vebby, apiad, karzym, Greg, ildiko, amitsowani, jkuo7, sth, han233ing
Comments
on 7. June 2021, 13:03 by Vebby
Very nice! Loved how the checkered constraint played out. Surprisingly tricky.. I struggled over this for some time because I overlooked one possibility for a region, but glad to come through! Thanks Panthera! :)


