Logic Masters Deutschland e.V.

Consider the below 5x5 toroidal latin square (each row and column has the numbers 1 to 5). On a torus, when you walk along a row you end up back to the start of that row. Whilst if you climb up a column, you end up back to the bottom of that column.

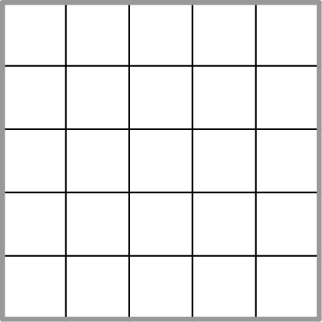
We can form a bagel by first gluing the top and bottom sides (to form a cylindrical surface), and then gluing the left and right sides (the two circular edges of the surface are then glued together). The gluing order matters.

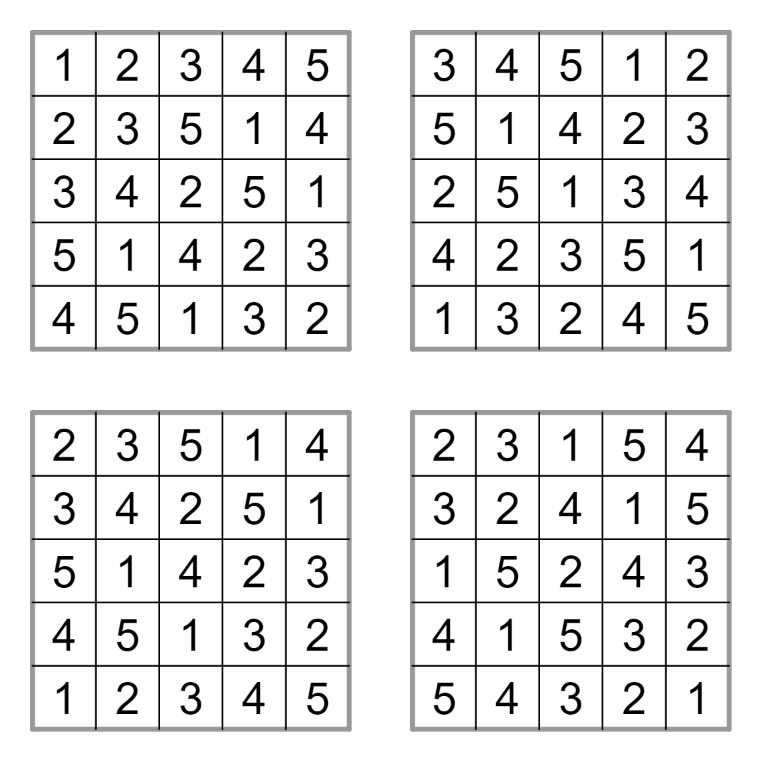
However, certain toroidal latin square grids give the same bagel. See the below examples of grids which give the same bagel (compositions of translations and 180 degree rotations).
In an anti-king bagel, each digit has the anti-king constraint. That is no two touching cells can have the same digit (touching at corners of the cells). This constraint is toroidal (is valid on the entire bagel unlike the above bagel).

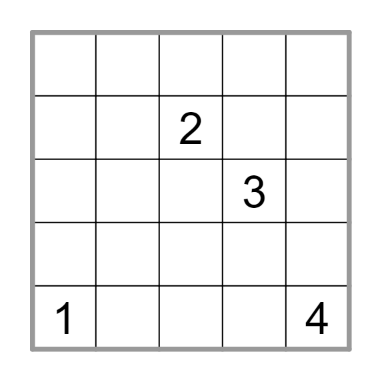
Your task will be to solve the below 5x5 anti-king bagel and count the number of distinct 5x5 anti-king bagels. Good luck!