Tetro Snake
(Eingestellt am 20. Juli 2020, 20:30 Uhr von Carrick22)
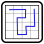
In diesem Rätsel müssen Sie eine Schlange (d.h. einen zellbreiten Weg) nach folgenden Regeln zeichnen:
- Die Schlange muss bei den beiden mit einem grauen Kreis markierten Zellen beginnen/enden.
- Die Schlange kann sich nicht orthogonal verzweigen oder sich selbst berühren (sie kann sich diagonal berühren).
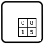
- Die von der Schlange unbenutzten Zellen müssen Flächen der Größe 4 bilden. Die Form dieser Bereiche kann jedes beliebige Tetromino sein (in der Ecke aufgelistet, kann gedreht werden). Diese Regionen können einander nicht orthogonal berühren.
- Die mit einem Buchstaben markierten Zellen müssen sich innerhalb eines Tetrominos befinden, das dem Buchstaben entspricht. Ein "?" kann jeden beliebigen Buchstaben bezeichnen.
Sie können Penpa-edit für interaktives Lösen.
Lösungscode: Zeile A, gefolgt von Zeile B. Verwenden Sie "1" für Schlange und den entsprechenden Buchstaben für eine Zelle innerhalb eines Tetrominos (Beispiel : 11JJJ11OO1).
Kommentare
am 21. Juli 2020, 07:51 Uhr von stefliew
@jwmpuz All cells that are not on the snake must belong to a tetromino. No tetromino can be orthogonally adjacent to another tetromino.
It's implied by "areas of size 4" that these areas cannot be touching each other otherwise they'd combine to form an area of a bigger size, but hopefully this clarifies the rules for you.
am 21. Juli 2020, 07:47 Uhr von jwmpuz
Either I'm confused (likely) or the instructions are missing a constraint. Based on my interpretation of the rules and the version of the (English-version) puzzle I see, the # of solutions seem limitless. See for example https://imgur.com/a/74iJEgT