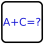Taxicab-kuro
(Eingestellt am 20. Juli 2020, 02:25 Uhr von glum_hippo)
Es gelten die üblichen Kakuro-Regeln. In jede Zelle ist eine Ziffer 1-9 so einzutragen, dass keine Ziffer in einem 'Wort' sich wiederholt, und die Ziffern sich zur gegebenen Summe zusammenzählen lassen.
Zusätzlich, als Hommage an Madmahogany, unterliegen alle Ziffern einer 'Manhattan distance' oder 'anti-taxicab' Einschränkung: wenn zwei Zellen dieselbe Ziffer enthalten, dann kann die Taxicab-Entfernung zwischen ihnen (die kleinste Anzahl orthogonaler Schritte zwischen zwei Punkten) nicht den Größenwert der Ziffer haben.
Beispiel: in der folgenden Abbildung ist wegen den vorgegebenen Ziffern die 7 von allen blau oder grün gefärbten Zellen, und die 4 von allen rot oder grün gefärbten Zellen ausgeschlossen. Wie man sieht, spielen die schwarzen Zellen bei der Errechnung der Manhattan Distance keine besondere Rolle. Bemerken Sie, daß die 7 auch in der obersten Reihe, gleiche Spalte, eine blaue Zelle erzeugt, sowie in derselben Reihe, sieben Stufen nach links! Man ist von Taxicab-Sudoku evtl. gewöhnt, Fortschreitungen in zwei Himmelsrichtungen abzusuchen.
Nun zum Rätsel. Die grauen Zellen helfen nur beim Abzählen und sind für die Logik unerheblich. Probieren Sie das Rätsel auch auf Penpa aus!
Lösungscode: Die erste Reihe und die letzte Spalte sind einzugeben. Die schwarzen Zellen werden ganz ausser Acht gelassen. (19 Ziffern insgesamt, wobei die Eckzelle ganz oben rechts zweimal eingegeben wird)
Kommentare
am 21. Juli 2020, 16:10 Uhr von mandourin
This is truly an incredible puzzle. Insanely hard too but so satisfying!
am 21. Juli 2020, 13:08 Uhr von glum_hippo
@Luigi Die 7 ist wegen Kakuro-Regeln von den senkrecht und waagerecht geformten ‘Worten’ ausgeschlossen, und wegen anti-Taxicab-Regeln von den entfernteren Zellen. Die weissen Zellen sind erlaubt weil sie einem anderen Wort angehören UND nicht genau sieben Zellen von der 7 Abstand halten.
am 21. Juli 2020, 08:51 Uhr von Luigi
Ich verstehe das Beispiel nicht. Die 7 ist von allen blau oder grün gefärbten Zellen ausgeschlossen. Bedeutet das, dass sie in den weißen, 4-6 Zellen darüber liegenden Zellen nicht ausgeschlossen ist?