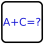Divisibility Squares Sudoku
(Eingestellt am 16. Juli 2020, 03:33 Uhr von ProwlingTiger)
Ich hatte die Idee dieses Puzzles schon lange und es war außerordentlich schwierig zu implementieren - aber ich habe endlich eines!
Es gelten die normalen Sudoku-Regeln. Zusätzlich hat jedes einzelne 4x4-Quadrat im Raster eine gerade Summe, und jedes einzelne 7x7-Quadrat hat eine Summe, die ein Vielfaches von 5 ist. Schließlich hat jedes der rosa 2x2-Quadrate auch eine gerade Summe.
Um die Regel weiter zu verdeutlichen, haben im folgenden Beispiel-Sudoku-Gitter alle möglichen 3x3-Quadrate (einschließlich der farbigen) eine durch 3 teilbare Summe. (Es gibt insgesamt 49 mögliche 3x3-Quadrate, die alle durch 3 teilbare Summen haben. ) Zum Beispiel ist im gelben Quadrat 9 + 7 + 2 + 1 + 2 + 6 + 4 + 5 + 9 = 45 durch 3 teilbar.
Und hier ist das eigentliche Rätsel. Ich könnte eine Datei oder eine kurze Zusammenfassung der (meiner Meinung nach wirklich coolen) Strategien veröffentlichen, die ich entdeckt habe, wenn ich herausfinden kann, wie.
Lösungscode: Zeile 5, dann Spalte 4.
Kommentare
am 17. Juni 2021, 19:14 Uhr von polar
Magnificent puzzle! Very rewarding indeed :)
am 19. September 2020, 04:54 Uhr von harrison
ProwlingTiger--this was an incredibly unique and difficult puzzle. I was very pleased and relieved to have finally solved it!
am 18. August 2020, 10:55 Uhr von joecat
Really nice puzzle - thank you!
am 9. August 2020, 18:29 Uhr von Jesper
I thought this was an amazing puzzle, requiring very interesting and original logic. Not easy to figure out, but very rewarding!
am 17. Juli 2020, 10:57 Uhr von MagnusJosefsson
Very nice and original puzzle, thank you!
am 16. Juli 2020, 19:12 Uhr von emmettcito
Lovely puzzle :) How were you able to set something like this, as that seems like that would be quite a challenge.
am 16. Juli 2020, 14:29 Uhr von SudokuExplorer
Wow! What a lovely puzzle! There is some really nice logic if you think about the geometry of the constraints. Congratulations for making one with such a clean solution path!
am 16. Juli 2020, 05:40 Uhr von ProwlingTiger
@RockyRoer: Good idea. Thanks for doing the puzzle! And I will certainly check your puzzles out and give them my best shot!
am 16. Juli 2020, 05:39 Uhr von RockyRoer
I'd also add the arithmetics needed tag.
am 16. Juli 2020, 05:30 Uhr von ProwlingTiger
@Greg: It was just an example.
am 16. Juli 2020, 05:30 Uhr von RockyRoer
@Prowling Tiger:
I enjoyed this a lot. Definitely 'cheated' by using a solver to help eliminate the possibilities, but that was no easy feat as you still had to determine how to determine what combinations of cells were odd, even, multiples of 5, 10, etc, but I still think I earned the solve :-) Feel free to hide this if you think this was giving away too much of a hint, but it was an enjoyable puzzle for sure. I hope others will enjoy it too.
Shameless plug... If you like this puzzle, you'll probably enjoy mine too -- some of the same math tricks would work, but I definitely learned some new ones doing yours. https://logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=0003U9
am 16. Juli 2020, 05:28 Uhr von Greg
Is the 3x3 always = 45 a rule that is used in the puzzle or did you just use it as a way of explaining the other rules?
am 16. Juli 2020, 04:25 Uhr von ProwlingTiger
Added title.
am 16. Juli 2020, 03:46 Uhr von RockyRoer
I hope you add a title to this so people can find it easier :-)