Longest Possible Palindrome - For Real This Time!
(Published on 13. June 2020, 12:32 by stephane.bura)
Comments on this puzzle made me realize that it was theoretically possible to have 73-cell long palindromes. Here's one.
This puzzle is not as pretty as the previous one but it should be a more interesting challenge... and it's 100% more accurate! ;)
Normal Sudoku rules apply.
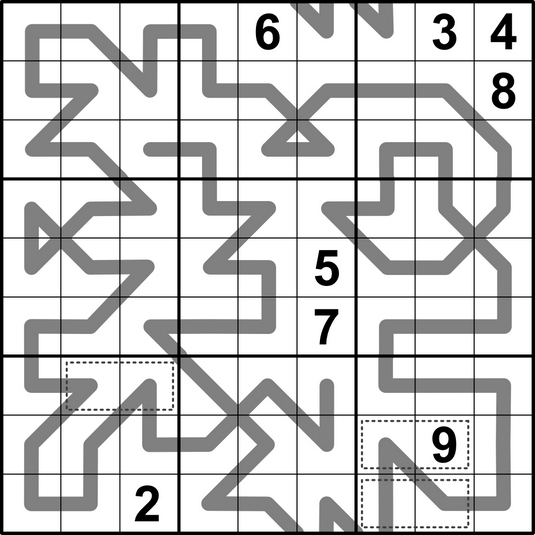
The gray line is a palindrome so, for instance, the digit in R3C4 is the same as the one in R8C6.
When the palindrome exits the grid, it continues on the opposite side. So the path it takes is R9C5-R1C6-R9C6-R1C7-R9C7.
Each dotted rectangle contains digits that add up to 15.
Penpa-Edit link for this puzzle to play it online.
This puzzle is not as pretty as the previous one but it should be a more interesting challenge... and it's 100% more accurate! ;)
Normal Sudoku rules apply.
The gray line is a palindrome so, for instance, the digit in R3C4 is the same as the one in R8C6.
When the palindrome exits the grid, it continues on the opposite side. So the path it takes is R9C5-R1C6-R9C6-R1C7-R9C7.
Each dotted rectangle contains digits that add up to 15.
Penpa-Edit link for this puzzle to play it online.
Solution code: Row 5, column 5
Last changed on on 13. June 2020, 15:41
Solved by Nothere, donut and chicken, dm_litv, Julianl, Joe Average, 0123coolkid, cdwg2000, Sebastian Losch, Narayana, saskia-daniela, Greg, keelyc27, Richard, Xavien , skywalker, Rollo, 111chrisi, lutzreimer, ... geronimo92, Zelytic, BenceJoful, Snowhare, ManuH, Mody, Uhu, rcg, Ours brun, MumboJumbo, Matt, starelev5, ParaNox, pipedreambomb, Raistlen, ildiko, zrbakhtiar, finger, Carolin, isajo4002
Comments
Last changed on 13. June 2020, 15:53
on 13. June 2020, 15:49 by stephane.bura
@0123coolkid Thanks :) Yes, because there is an odd number of copies of each digit. So at most you can have a palindrome of 9 x 8 + 1 cells, where the extra cell is at the center.
on 13. June 2020, 15:44 by 0123coolkid
I thought this was going to be super annoying at first, but once I was knee deep in the puzzle it was pretty great. Cool puzzle! What's the largest possible palindromic sequence in a sudoku? Is it in fact 73?
on 13. June 2020, 15:41 by stephane.bura
Fixed spelling.