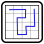
Roller Coaster mit Extras 7
(Eingestellt am 25. Juni 2018, 15:32 Uhr von Uhu)
Zeichne auch einen Rundweg durch einige Zellen ein, der die Mittelpunkte benachbarter Zellen verbindet und sich nicht selbst kreuzt.
Zahlen, die links außerhalb stehen, geben die Summe von Ziffern in dieser Zeile an (in der richtigen Reihenfolge). Jede Summe liegt auf einem waagrechten Wegsegment, wobei ein Wegsegment von einer Abbiegung bis zur nächsten Abbiegung geht.
Zahlen, die oben außerhalb stehen, geben die Summe von Ziffern in der darunterliegenden Spalte an (in der richtigen Reihenfolge). Jede Summe liegt auf einem senkrechten Wegsegment, wobei ein Wegsegment von einer Abbiegung bis zur nächsten Abbiegung geht.
Es sind alle Summen gegeben.
Ein Punkt '.' steht für eine beliebige Ziffer von 0 - 9. Eine zweistellige Summe kann nicht mit einer '0' beginnen (muss also größer oder gleich 10 sein).
Zusätzlich gilt:
-) Der Rundweg kann auch diagonal benachbarte Zellen miteinander verbinden, allerdings muss dies durch einen orangefarbenen Punkt gekennzeichnet sein.
-) Wenn der Rundweg diagonal abbiegt, darf er nicht sofort wieder einen orangefarbenen Punkt verwenden. Sprich: er muss nach einem diagonalen Wegsegment waagrecht oder senkrecht weiterverlaufen, bevor der nächste Punkt verwendet werden darf.
-) Alle orangefarbenen Punkte müssen verwendet werden.
-) Alle orangefarbenen Punkte sind vorgegeben.
Lösungscode: Zeile 2 und Spalte 4.
Kommentare
am 11. September 2024, 23:13 Uhr von Christounet
Very nice !
One advice for future solvers : read the rules VERY carefully for this one. There is one sentence that may be overlooked, which cost me to be stuck for quite some time...
am 16. August 2024, 05:15 Uhr von Nick Smirnov
Penpa+ (with rules in English):
https://tinyurl.com/25wovppm
am 1. Mai 2023, 16:00 Uhr von Lucx
Wahrlich, was die Diagonalen alles ändern. Da hatte ich schon ein paar Mal ein “Moment, das geht doch gar nicht…”. - vielen Dank!
am 15. August 2018, 12:41 Uhr von ffricke
Wieder super, der Einstieg fiel ein wenig schwer, doch dann war die Fahrt inklusive der Diagonalen richtig spritzig.
am 8. August 2018, 15:50 Uhr von flaemmchen
Wie diese Diagonalen doch alles verändern ;-)
Tolles Rätsel!
am 8. Juli 2018, 16:36 Uhr von Mody
Kniffelig, aber total schön
am 28. Juni 2018, 12:27 Uhr von ibag
Mal wieder echt klasse!
am 27. Juni 2018, 15:55 Uhr von Statistica
Klasse und echt knackig!
am 26. Juni 2018, 18:11 Uhr von jalbert
Fun!!
am 26. Juni 2018, 08:50 Uhr von ch1983
Wieder toll, vielen Dank.
am 25. Juni 2018, 23:39 Uhr von marcmees
nice series.
can't stop at 7.