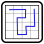
Rätsel im Advent (13): Tapasyu
(Eingestellt am 13. Dezember 2015, 09:00 Uhr von usp)
Zeichne einen Rundweg in das Gitter, der senkrecht oder waagerecht von Feldmittelpunkt zu Feldmittelpunkt verläuft und jedes Feld maximal einmal durchquert.
Felder mit Kreisen müssen vom Rundweg benutzt werden. Kreise können gefärbt werden. In weißen Kreisen führt der Weg geradeaus, knickt aber im Feld davor oder dahinter im rechten Winkel ab. In gefärbten Kreisen knickt der Weg im rechten Winkel ab und führt in den beiden auf dem Weg benachbarten Feldern geradeaus weiter.
Durch Felder mit Zahlen führt der Weg nicht. Eine Zahl gibt an, wieviele der angrenzenden Felder vom Rundweg benutzt werden. Diese Felder müssen senkrecht oder waagerecht nebeneinanderliegen, aber nicht unbedingt einen zusammenhängenden Teil des Rundweges bilden. Zwischen verschiedenen Gruppen von Rundwegfeldern rund um ein Zahlfeld muss mindestens ein leeres Feld liegen.
Lösungscode: Für jede Spalte von links nach rechts die Länge der längsten senkrechten Linie
Kommentare
am 14. Dezember 2015, 10:06 Uhr von usp
;-)
am 14. Dezember 2015, 09:45 Uhr von Statistica
Wieso? Der 14. ist nur im Februar der Valentinstag <3
am 13. Dezember 2015, 14:41 Uhr von CHalb
Ich finde, dieses Rätsel kommt mindestens einen Tag zu früh ;-).
am 13. Dezember 2015, 09:17 Uhr von Luigi
Da haben wohl wieder einige pünktlichst ihr Türchen geöffnet... ;-))