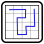
Odd Tapasyu
(Eingestellt am 29. Oktober 2014, 00:00 Uhr von usp)
Es gelten die Regel des variablen Tapasyus (siehe unten).
Allerdings müssen bei dieser Variante die Hinweiszahlen rekonstruiert werden. Alle Zahlen sind ungleich 0. Jede 0 steht für eine gerade Zahl, jede 1 für eine ungerade Zahl. Fragezeichen können durch beliebige Zahlen ersetzt werden.
Zeichne einen Rundweg in das Gitter, der senkrecht oder waagerecht von Feldmittelpunkt zu Feldmittelpunkt verläuft und jedes Feld maximal einmal durchquert.
Felder mit Kreisen müssen vom Rundweg benutzt werden. Kreise können gefärbt werden. In weißen Kreisen führt der Weg geradeaus, knickt aber im Feld davor oder dahinter im rechten Winkel ab. In gefärbten Kreisen knickt der Weg im rechten Winkel ab und führt in den beiden auf dem Weg benachbarten Feldern geradeaus weiter.
Durch Felder mit Zahlen führt der Weg nicht. Eine Zahl gibt an, wieviele der angrenzenden Felder vom Rundweg benutzt werden. Diese Felder müssen senkrecht oder waagerecht nebeneinanderliegen, aber nicht unbedingt einen zusammenhängenden Teil des Rundweges bilden. Zwischen verschiedenen Gruppen von Rundwegfeldern rund um ein Zahlfeld muss mindestens ein leeres Feld liegen.
Lösungscode: Die Anzahl der gefärbten Kreise in jedem der drei aus Kreisen geformten Buchstaben, gefolgt von den Längen aller waagerechten Linien in der mittleren Zeile.
Kommentare
am 26. November 2014, 17:51 Uhr von HaSe
again: herausragend
am 3. November 2014, 13:50 Uhr von usp
@zorant: 1 can also be replaced by 1 (this is an odd number, too).
am 3. November 2014, 12:32 Uhr von ffricke
Mir gings erst wie Gabi, aber dann sah ich den Einstieg und es lief flüssig. Diese Tapasyus sind ein Genuss!
am 2. November 2014, 19:28 Uhr von zorant
Hi,
Does the number 1 can only be replaced with 3,5,7 or can remain "1"?
am 2. November 2014, 08:42 Uhr von ibag
Großartig!!! Am Anfang dachte ich, da geht gar nichts ...
am 29. Oktober 2014, 12:31 Uhr von Katrin K
Einfach toll!
am 29. Oktober 2014, 05:19 Uhr von r45
Noch mehr suuuuper! ;-)