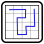
Toroidales Tapasyu 2
(Eingestellt am 25. Oktober 2014, 00:00 Uhr von usp)
Es gelten die Regeln des variablen Tapasyus (siehe unten).
Zusätzlich stellt bei dieser Variante das Diagramm einen Torus dar, d. h. der rechte und linke sowie der obere und untere Rand sind jeweils verbunden.
Zeichne einen Rundweg in das Gitter, der senkrecht oder waagerecht von Feldmittelpunkt zu Feldmittelpunkt verläuft und jedes Feld maximal einmal durchquert.
Felder mit Kreisen müssen vom Rundweg benutzt werden. Kreise können gefärbt werden. In weißen Kreisen führt der Weg geradeaus, knickt aber im Feld davor oder dahinter im rechten Winkel ab. In gefärbten Kreisen knickt der Weg im rechten Winkel ab und führt in den beiden auf dem Weg benachbarten Feldern geradeaus weiter.
Durch Felder mit Zahlen führt der Weg nicht. Eine Zahl gibt an, wieviele der angrenzenden Felder vom Rundweg benutzt werden. Diese Felder müssen senkrecht oder waagerecht nebeneinanderliegen, aber nicht unbedingt einen zusammenhängenden Teil des Rundweges bilden. Zwischen verschiedenen Gruppen von Rundwegfeldern rund um ein Zahlfeld muss mindestens ein leeres Feld liegen.
Lösungscode: Die Anzahl der gefärbten Kreise in jedem 'T' im Uhrzeigersinn, beginnend mit dem 'T' oben links; gefolgt von der Anzahl der Linien, die den oberen und den rechten Rand des Diagramms kreuzen (insgesamt 6 Zahlen)
Kommentare
am 27. Juni 2024, 00:02 Uhr von DiMono
I made a URL to solve on Penpa+: https://tinyurl.com/budbwb5e
Note: for the solution check to work, you should use green for the line, and where the line wraps around, it should be drawn leaving the grid on both sides.
am 4. Mai 2015, 12:30 Uhr von Rollo
extreme toroidaling :-) :-) :-)
am 30. Oktober 2014, 13:50 Uhr von Statistica
Mal wieder klasse! Danke!!
am 27. Oktober 2014, 09:31 Uhr von CHalb
Sehr beeindruckend. Erst mitten beim Lösen hab ich registriert, dass die wie immer nicht im Überfluss vorhandenen Hinweise obendrein auch noch symmetrisch angeordnet sind. Toroidale Rätsel sind für mich bei Rundwegen so eine Art Königsdisziplin, weil die Extrembereiche Rand und Ecken völlig aufgehoben werden. Und dieses Rätsel nutzt das voll aus; ich finde den Wegverlauf an den Kanten und Ecken sozusagen "sehr toroidal". Und das ganze ist echt interessant, schön schwierig und mir ist nur an einer Stelle ein Eindeutigkeitsschluss aufgefallen.
am 25. Oktober 2014, 22:14 Uhr von Senor Dingdong
Schön bis zum Ende!
am 25. Oktober 2014, 12:08 Uhr von ibag
Das konnte man echt nicht wieder aus der Hand legen! Danke!
am 25. Oktober 2014, 09:13 Uhr von Alex
und ich auch, tolle Serie ueberhaupt.
am 25. Oktober 2014, 08:21 Uhr von Luigi
Dem kann ich mich nur anschließen!
am 25. Oktober 2014, 06:51 Uhr von r45
Suuuuper!