Bosnian Road
(Eingestellt am 25. Oktober 2013, 12:00 Uhr von Richard)
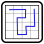
Beispiel:
Rätsel:
Original idea for this puzzle: Dragan Tolomanoski
Lösungscode: Die Anzahl der vom Rundweg durchlaufenen Kästchen, Zeile für Zeile (im Beispiel 43324).
Kommentare
am 30. Mai 2022, 18:49 Uhr von Nick Smirnov
Penpa:
https://tinyurl.com/2h5jzbxo
am 30. Mai 2022, 18:07 Uhr von Nick Smirnov
@Richard, the road can't go through cells with numbers, right?
Edit: I assumed this condition and solved both puzzles, so it is probably correct.
am 4. August 2021, 12:44 Uhr von Dandelo
Das gehört eher ins Forum, aber kann man nicht einfach sagen:
Schwärze einige Felder, so dass es nur einen Weg vom Kopf bis zum Schwanz gibt. Alle geschwärzten Felder müssen auf dem Weg liegen und alle ungeschwärzten mit dem Rand verbunden sein. Evtl. Mit dem Zusatz 'orthogonal'.
am 4. August 2021, 12:34 Uhr von Dandelo
Bei Korallen und Höhlen macht man das doch auch über die unbenutzten Felder. Ist eine Schlange nicht einfach eine Koralle ohne Abzweigungen?
am 4. August 2021, 12:27 Uhr von Dandelo
Da müsste man dann verlangen, dass die unbenutzten Felder zusammenhängen. Da muss man natürlich das große Außengebiet mitbetrachten.
Oder dass es kein zusammenhängendes Gebiet aus leeren Feldern gibt, das nur an Schlangenfelder grenzt.
Jeweils plus die 2x2-Bedingung.
Ist jetzt nicht unbedingt einfacher zu lesen, aber die Interpretationsmöglichkeiten fallen weg.
am 4. August 2021, 12:06 Uhr von uvo
Das müsste hier auch gehen, funktioniert aber bei Schlangen nicht.
am 4. August 2021, 11:36 Uhr von Dandelo
Kann man nicht auch sagen, die Felder im Inneren müssen orthogonal zusammenhängen und kein 2x2-Bereich darf komplett belegt sein? Da gäbe es keinen Interpretationsspielraum.
am 4. August 2021, 11:16 Uhr von uvo
@Dugong: In der Anleitung steht "... und sich selbst nicht berührt".
Problematisch ist allerdings, dass diese Formulierung in verschiedenen Situationen unterschiedlich gebraucht wird. Gelegentlich ist damit gemeint, dass der Rundweg jedes Feld höchstens einmal betritt: es wäre ja denkbar, dass ein Rundweg im selben Feld einmal von links kommend nach unten abbiegt und einmal von rechts kommend nach oben abbiegt. Die Formulierung "berührt sich nicht selbst" verbietet dies.
Im aktuellen Rätsel, das eher mit Schlangen verwandt ist, soll die Formulierung aber folgendes bedeuten: würde man die Felder entlang des Rundwegs nummerieren, so dürfen orthogonal/diagonal benachbarte Felder nur dann beide zum Rundweg gehören, wenn die Feldnummern die Differenz 1 bzw. 2 haben.
am 4. August 2021, 10:29 Uhr von Dugong
Keine Diagonale Eigenberührung. Ziemlich standard, aber sollte auch ausgeschrieben werden.
am 28. Oktober 2013, 10:33 Uhr von Rollo
Es müsste noch erwähnt werden, dass der Rundweg nicht durch Zahlenfelder geht.