Schlingerpfad 5x5
(Eingestellt am 3. Juli 2012, 21:42 Uhr von adam001)
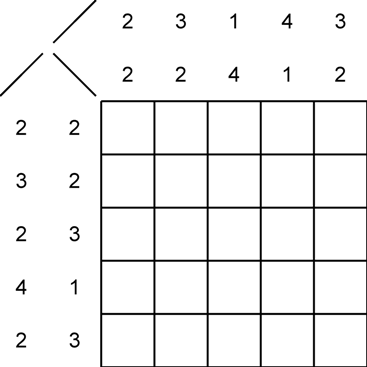
Zeichne einen Pfad, dessen Wände Diagonalen in den Feldern sind. Der Pfad hat zwei Enden am Rand des Diagramms, verzweigt sich nicht und hat immer die gleiche Breite. Die Zahlen am Rand geben an, wie oft die entsprechenden Diagonalen in der Zeile oder Spalte vorkommen. Jede Diagonale soll eine Wand des Pfades sein.
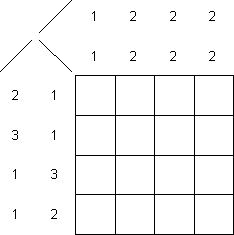
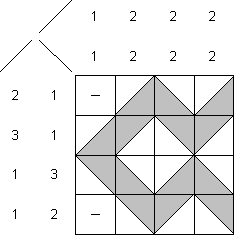
Eine Beispielaufgabe (Lösung mit grau markiertem Pfad):
Andere Rätsel dieser Art: 7x7, 7x7S (Variant) 8x8, 9x9, 11x10.
Eine Beispielaufgabe (Lösung mit grau markiertem Pfad):
© adam001
Andere Rätsel dieser Art: 7x7, 7x7S (Variant) 8x8, 9x9, 11x10.
Lösungscode: Die zehn Zeichen der zweite und fünfte Zeile
Ersetze / durch 1, durch 2 und - durch 0.
Zuletzt geändert am 1. November 2020, 10:53 Uhr
Gelöst von Skinny Norris, Kekes, Zzzyxas, moss, Luigi, Toastbrot, dm_litv, Statistica, Laje6, ibag, ffricke, pokerke, HaSe, ch1983, saskia-daniela, Alex, Eisbär, lutzreimer, StefanSch, MiR, rimodech, Mody, ... Rollie, CHalb, kiwijam, flaemmchen, BFaw, martin1456, lupo, ManuH, relzzup, Rollo, Mars, sandmoppe, Ute2, PRW, AnnaTh, matter, sf2l, uvo, tuace, Joe Average, ildiko, jessica6, H1324851344, cdwg2000
Kommentare
am 1. November 2020, 10:53 Uhr von adam001
tags placed
am 10. Oktober 2014, 12:27 Uhr von uvo
Ehrlich gesagt, finde ich das Beispiel ziemlich irreführend, es suggeriert nämlich, daß von jedem Feld (mit Ausnahme der Leerfelder) genau eine Hälfte Teil des Pfads ist.
am 3. Oktober 2012, 21:10 Uhr von adam001
Bei janko.at gibt es auch eine Serie Schlingerpfadrätsel unter dem Namen Mäander.