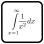Logic Masters Deutschland e.V.

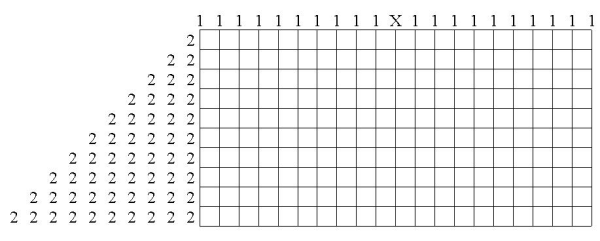
1. Die Zahlen oberhalb des Diagramms geben an, wie viele Wassertropfen in der jeweiligen Spalte (entlang der Gitterlinien) ins Diagramm hineinfallen, dabei ist eine Zahl (X) unbekannt. Ebenfalls unbekannt ist die Anzahl der Tropfen, die unten am Diagramm austreten.
2. Solange ein Tropfen nicht auf einen Schirm trifft, fällt er senkrecht.
3. Trifft ein Tropfen links der Mitte auf einen Schirm, so läuft er zum linken Rand des Schirms; trifft er rechts der Mitte auf einen Schirm, so läuft er zum rechten Rand. In beiden Fällen tropft er danach senkrecht nach unten.
4. Bei Schirmen mit einer geraden Breite dürfen exakt in der Mitte nur eine gerade Anzahl an Tropfen auftreffen. Eine Hälfte der Tropfen läuft dann zum linken, die andere zum rechten Rand des Schirms.

Die Regenschirme sind jeweils ein Kästchen hoch und haben verschiedene Breiten; die Zahlen links des Diagramms geben an, welche Schirmbreiten in der entsprechenden Zeile vorkommen, bei mehreren Schirmen in einer Zeile auch in der entsprechenden Reihenfolge. Die Schirme dürfen einander beliebig berühren, jedoch nicht überschneiden, also kein Kästchen gemeinsam benutzen.

Welche Zahlen können für X eingesetzt werden?