135 Cubedoku
(Published on 12. November 2024, 12:49 by Chilly)
This is the next in my Cubedoku series. You can find the first puzzle, here, and the second puzzle here.
This one is a variant on broken 159 - broken 135.
135 Cubedoku
by Chilly
The Rules:
- Standard Cubedoku rules apply. Fill the cells with the digits 1-5, so that each face of the cube is a valid Sudoku grid. Every digit in each grid indexes a 1x1x1 target cell within the cube, and each target cell must be indexed by all three grids.The digit 1 in a cell specifies that the target cell is the 1x1x1 cube closest to the surface of the cube where the digit is located, whereas a digit 2 in a cell indicates that the target cell is the second cube down from the surface, and so on.
- Broken 135 rules apply: digits in red cells in columns 1, 3 and 5 indicate the position of the 1, 3 and 5 respectively in their corresponding row - all possible red cells are given so if a cell in column 1, 3 or 5 is not red it must NOT correctly index the position of the appropriate digit. The columns are numbered in the direction of the arrows.
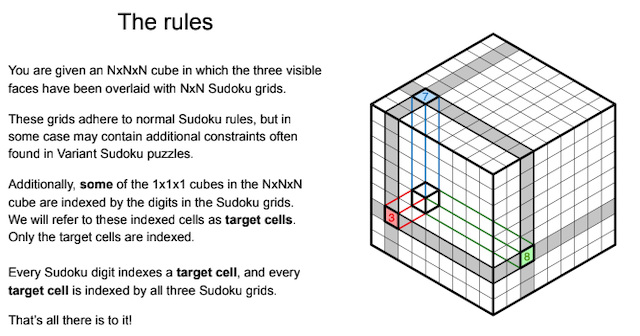
The rules are a little complicated, so I'm including the first picture below (courtesy of Andrewsarchus) to show how it works. You can see that entering a digit on one face of the grid determines which single internal 1x1x1 cube is indexed (the target cell), and that cube has to be indexed by all the other faces, putting a further digit on all the remaining faces. There are three visible faces, the digits on all of which are constrained by their indexing connections to the internal 1x1x1 cubes, but also to any Sudoku constraints we place on the surfaces of these faces (e.g. irregular regions, thermos or other standard Sudoku variants). This can lead to some new and interesting interactions. To solve the puzzle, we need to place digits in all cells of the three visible faces. If the faces are 4x4, we use the digits 1-4, or if they are 6x6 we use the digits 1-6, etc. just like normal Sudoku puzzles.
Solution code: Cells along the perimeter of the top face in clockwise order beginning at the top of the image. (16 digits, no spaces)
Solved by kublai, marcmees, Andrewsarchus
Comments
on 13. November 2024, 09:47 by marcmees
very approachable. Thanks




