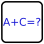Logic Masters Deutschland e.V.

Short summary of the rules is given here. The full, clear explanation can be read in this file. The file also includes an illustration of how the ruleset works, a few hints and a full walkthrough if you get stuck!

In general, in this candle-lit puzzle you have to find where all the killer cages are and what their sums will be. You have to obey some negative restrictions.

Every row contains a one-cell-tall killer cage. All the cages are orthogonally connected. The sums of the cages are the powers of x from the 0th to the nth where x and n are integers that have to be determined by the solver. There is one cage per different counts of digits that can be used to make up each sum. E.g. if one of the sums is 6, that can be made up of 1, 2 or 3 digits, so there will be three cages with the sum 6.

The cages are ordered from lowest sums at the bottom to highest sums at the top of the grid. Within each set of cages with the same sum, the cages that have less digits inside are further down. (e.g. 6 in 1, then 6 in 2, then 6 in 3)

The cages divide the rest of the grid into four regions. Some three of these regions contain x, 2n, and 3x + n cells respectively.

Black kropki dots mark cells that have digits with the ratio 1:2 in them. In addition, if a cage fully contains at least one black dot, a partition can be placed somewhere inside the cage so that the sums of the digits on either side of the partition are also in a 1:2 ratio.

Negative restrictions: Cells without dots between cannot be in a ratio of 1:2. Cages without a black dot fully inside cannot be possible to partition in the ratio 1:2.

The three-cell line is a modular line. No three digits along the line can have the same mod(3) value. (They must contain one digit from each set 1-4-7, 2-5-8 and 3-6-9.)