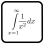Eleven, not five
(Published on 25. March 2024, 20:26 by FunkySalad)
Every 3-digit number formed by a row, a column and a negative diagonal of boxes 1, 5 and 9 is divisible by 11. For example, r4c4 r5c5 r6c6 can't be 1, 3 and 7 respectively because then the negative diagonal of box 5 forms a 3-digit number 137 which is not divisible by 11.
Cells divided by a black dot contain digits in a 1:2 ratio.
Digits in orthogonally adjacent cells must not add up to 5.
f-puzzles
This is my first sudoku, so I would really appreciate your feedback!
Solution code: Row 6, column 7 (18 characters, no spaces).
Comments
on 25. March 2024, 22:31 by FunkySalad
@ymhsbmbesitwf, thanks for your feedback, added your example to description.
on 25. March 2024, 22:23 by FunkySalad
I was afraid that this rule might be a little confusing :-) Basically, when you look at a box separately, each its row forms a 3-digit number that should be read from left to right. Each box's column can also be considered as a 3-digit number when read from top to bottom. Also digits on a negative diagonal of a box form a 3-digit number read from top-left to bottom-right corner. All these 3-digit numbers for boxes 1, 5 and 9 must be divisible by 11 (for example, cells 1 to 3 in row 1 can contain 3, 5 and 2, so 352=11*32). I hope it helps :-)
on 25. March 2024, 22:19 by ymhsbmbesitwf
As a whole a bit grindy, but the negative V constraint is quite satisfying.
The rules are well worded, though with the first rule being far from standard it's always nice to have some examples: r4c4 r5c5 r6c6 can't be 1, 3 and 7 respectively because then the negative diagonal of box 5 forms a 3-digit number 137 which is not divisible by 11.
on 25. March 2024, 21:56 by Big Tiger
I'm not quite understanding the 11's. Clarification would be appreciated. :-)