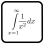Logic Masters Deutschland e.V.

This is a 9*9 version of my previous idea. This time, I add an anti-king constraint to keep the layout simple (the modifiers don't have an anti-king constraint), and this allows for some new logic. Hope you enjoy!

Rules:

• Normal Sudoku rules apply. Place the digits 1-9 once in every row, column, and box.
• Modifiers: There are 9 types of modifiers, each modifying the value of a digit for the purposes of arrows. Each type of modifiers appears in every row, column, and box. No two or more modifiers may occupy the same cell. The modifiers apply the following operations to the digit n：
• 1. n*1     2. n*2     3. n*3
• 4. n*4     5. n*5     6. n*6
• 7. n*7     8. n*8     9. n*9
• Anti-king: Cells a king's move away from each other may not contain the same digit. (But they may contain the same type of modifiers.)
• Arrow: The values of cells on an arrow must sum to the value of the cell in the corresponding circle. For the lines, either end of the line may be the circle of the arrow, which must be determined by the solver.

Links:

Multiple grids:     CTC     Penpa

Single grid:     CTC     Penpa

Like the previous one, this one requires some mathematical tricks including 'Rearrangement Inequality', which gives the minimum and maximum of the sum of pairwise products of two sequences. (Highlight to see the trick)

Leave a comment to let me know how hard you will rate the puzzle.

Example

The following image is an example of a valid grid of 6x6. It is not a playable puzzle; it is only intended for demonstration purposes.