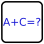Parity Party XXIV, "Fast Times"
(Published on 30. November 2022, 17:14 by glum_hippo)
Normal Chaos Construction rules apply. Each row, column, and thick-bordered 9-cell region must contain the digits 1-9 exactly once each. However, the regions must be determined by the solver. One edge of a region is already given.
Clues outside the grid are both Border Sum and Parity Party clues.
(1) They indicate both the sum of the two digits straddling the first-seen border from that vantage point, AND
(2) they give the sum of cells encountered when moving through the grid from that vantage point, UP TO AND INCLUDING the first odd or first even digit. For example, a 15 at the bottom of a column could indicate something like 7-8, 8-7, 1-3-5-6 or 2-6-4-3 (among others) when reading up that column... but not 1-2-3-4-5 or 2-6-3-4 etc. That is, the parity of the farthest digit must deviate from that of the others. Note: If a parity party clue is less than 10, it could be fulfilled by a single digit, i.e., the sum of zero odds and one even, or zero evens and one odd.
A '?' can stand for any single positive integer. Above column 4 there is also a single positive integer less than 14.
Solution code: Row 8, then column 3, then the number of borders between regions that are traversed in each row. (27 digits total)
Comments
on 10. March 2023, 22:13 by Zombie Hunter
Once I got past my functional fixedness the puzzle fell into place. I look forward to solving more in this series. Wonderful construction.
on 7. December 2022, 10:56 by MagnusJosefsson
Fun and challenging! Very nice to see a new Parity Party puzzle again.
Thank you for your kind words, Magnus. I’ll be publishing one more puzzle in this series at the end of December
on 4. December 2022, 09:41 by PixelPlucker
Rather pleased indeed, thanks hippo
<3 glad you enjoyed it, Pixy
on 1. December 2022, 06:37 by marcmees
enjoyed that. thanks.
Thank you also! I am grateful for your attention to this puzzle