Cylic Modular Casscade

(Published on 22. September 2022, 09:06 by glenfletcher)

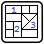
Unless explicitly stated, rules apply to the toroid grid formed by allowing the provided grid to wrap around both horizontally and vertically.
Digits must not repeat in a region.
Digits must form the same 9-cycle across each row.
For every 4-length subsequence of the 9-cycle across each row, the sum of the first and last digits must be congruent modulo 9 with the sum of the middle two digits. (i.e. R1C9 + R1C3 ≡ R1C1 + R1C2 (mod 9)).
The sum of the forward differences modulo 9 between all unique pairs in the 9-cycle across each row must be minimised, subject to the other rules. (i.e. (R1C1 – R1C9 (mod 9)) + (R1C2 – R1C1 (mod 9)) + … + (R1C9 – R1C8 (mod 9)) must be minimized).
Digits must form the same 9-cycle down each column.
Digits must form the same 9-cycle up each positive diagonal.
Digits must not be congruent modulo 3 with digits orthogonal adjacent or adjacent along any positive diagonal. (i.e. the following must all be false, R3C4 ≡ R2C4 (mod 3), R3C4 ≡ R4C4 (mod 3), R3C4 ≡ R3C3 (mod 3), R3C4 ≡ R3C5 (mod 3), R3C4 ≡ R2C5 (mod 3) and R3C4 ≡ R4C3 (mod 3)).
Digits must form a recurring 3-cycle composed of those digits congruent modulo 3 along negative diagonals, and the cycle must be the same cycle for each group of digits that are congruent modulo 3. (i.e. R1C4 ≡ R2C5 ≡ R3C6 (mod 3) but R1C4 ≠ R2C5 ≠ R3C6 ≠ R4C7 = R1C4).
The values (A and B) indicated down the side of the grid are the sum of digits between (1 and 9) in the provided grid, and have a difference of 5.