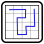
Chaos Construction: Arukone
(Published on 17. April 2022, 01:27 by Dandelo)
Then draw lines that go from field center to field center and begin and end in the fields marked with circles. All fields and all areas are entered exactly once.
Example with numbers from 1 to 5:(penpa+)
Solution code: Row 5 and column 4
Comments
on 20. April 2022, 16:00 by Dandelo
Yes, I knew that the rules could be misinterpreted (though I still think that "all fields and all areas are entered exactly once" says everything). But the example should leave no questions open, I hoped.
on 20. April 2022, 15:32 by MagnusJosefsson
Great puzzle! Very fun and also quite approachable in retrospect, although I got stuck at one point after making an unfounded assumption about the ruleset [your first comment below resolved it :)].
on 17. April 2022, 17:02 by marcmees
quite straightforward. Well constructed.
Thanks
on 17. April 2022, 11:54 by Dandelo
Link zum Beispiel ergänzt
on 17. April 2022, 10:17 by Dandelo
I noticed that my (very easy) example was broken, and had to replace it quickly, at 2:00 a.m. ...
The solution path is very straightforward, if you find the intended break-in. I'd claim, after the break-in there's only one point (when finishing the regions), where you have to take a deeper look, but no T&E.
on 17. April 2022, 09:50 by cmb
Beautiful puzzle!
on 17. April 2022, 02:04 by Dandelo
Nicht eindeutiges Beispiel ersetzt.
on 17. April 2022, 01:03 by Dandelo
Anders formuliert:
Jeder Weg beginnt in einem Kreisfeld, durchläuft dann alle Felder des Gebietes mit diesem Kreisfeld, betritt dann möglicherweise ein anderes Gebiet, durchläuft auch dort alle Felder, wiederholt diesen Vorgang beliebig oft und endet dann in einem Kreisfeld, das er in dessen Gebiet als letztes Feld betritt.
In other words:
Each path starts in a field with a circle, then enters all fields of the area with this circle field, then possibly enters another area, also enters all fields there, repeats this process as often as you like and then ends in a circle field, which it enters as the last field of this area.