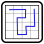
Beispiel für Roller Coaster mit Extras 25
(Published on 3. March 2022, 06:35 by Uhu)
Platziere die Ziffern von 1 bis 6 in jede Zeile und in jede Spalte innerhalb jedes 6x6-Diagramms. (mögliche Ausnahme siehe unten)
Zeichne auch einen Rundweg durch einige Zellen ein, der die Mittelpunkte orthogonal benachbarter Zellen verbindet und sich nicht selbst kreuzt. (mögliche Ausnahme siehe unten)
Es gibt nur einen Rundweg, der durch jedes Diagramm mindestens einmal führt und die Diagrammsgrenzen beliebig oft übertreten kann.
Zahlen, die links bzw. rechts außerhalb stehen, geben die Summe von Ziffern in dieser Zeile an (in der richtigen Reihenfolge). Jede Summe liegt auf einem waagrechten Wegsegment, wobei ein Wegsegment von einer Abbiegung bis zur nächsten Abbiegung geht oder, wenn der Weg die Diagrammsgrenze übertritt, dann geht ein Wegsegment von einer Abbiegung bis zur Diagrammsgrenze.
Zahlen, die oben bzw. unten außerhalb stehen, geben die Summe von Ziffern in dieser Spalte an (in der richtigen Reihenfolge). Jede Summe liegt auf einem senkrechten Wegsegment, wobei ein Wegsegment von einer Abbiegung bis zur nächsten Abbiegung geht oder, wenn der Weg die Diagrammsgrenze übertritt, dann geht ein Wegsegment von einer Abbiegung bis zur Diagrammsgrenze.
Es sind alle Summen gegeben.
Ein Punkt '.' steht für eine beliebige Ziffer von 0 - 9. Eine zweistellige Summe kann nicht mit einer '0' beginnen (muss also größer oder gleich 10 sein).
Gleiche Ziffern dürfen sich über Diagrammsgrenzen hinweg nicht orthogonal berühren.
Ordne jedem Diagramm genau eine der folgenden Ausnahmen zu, jede Regel maximal einmal:
- Ausnahme 1:
Der Weg darf sich kreuzen und muss sich auch mindestens einmal kreuzen.
Auf einer Kreuzung geht der Weg geradeaus hindurch - der Weg darf auf einer Kreuzung nicht abbiegen.
Das gelb eingefärbte Feld kann vom Weg benutzt werden oder nicht.
- Ausnahme 2:
Einige Felder sind eingefärbt. Diese Felder dürfen vom Rundweg nicht benutzt werden.
- Ausnahme 3:
Platziere die Ziffern von 0 bis 6 in jede Zeile und in jede Spalte innerhalb des 6x6-Diagramms.
Es gibt in jeder Zeile bzw. Spalte ein gefärbtes Feld, in welches ein 'Spiegel', der vom Weg benutzt werden muss, einzuzeichnen ist. Die Spiegel führen von einer Ecke eines gefärbten Feldes zur schräg gegenüberliegenden Ecke.
Ein Spiegel lenkt den Weg um 90° ab.
In jedem gefärbten Feld sind 2 Ziffern einzutragen, wobei nur eine Ziffer vom Weg benutzt wird.
Ziffern, die in den gefärbten Feldern stehen und nicht vom Weg benutzt werden, sind alle verschieden.
Es sind nicht alle gefärbten Felder gegeben, einige müssen selbst herausgefunden werden.
- Ausnahme 4:
Entlang des Rundwegs muss die Wurmregel beachtet werden - die Ziffern müssen abwechselnd größer und kleiner werden.
Das gelb eingefärbte Feld kann vom Weg benutzt werden oder nicht.
- Ausnahme 5:
Es gelten die üblichen Sudoku-Regeln: Die Ziffern von 1 bis 6 müssen zusätzlich in jedem fett umrandeten Gebiet genau einmal vorkommen.
Die Gebietsgrenzen des Sudokus müssen selbst eingezeichnet werden - entweder 2x3-Boxen oder 3x2-Boxen.
Das gelb eingefärbte Feld kann vom Weg benutzt werden oder nicht.
Solution code: Zeile 5 und Zeile 8.
Comments
on 14. October 2024, 15:33 by Nick Smirnov
Penpa+ (with rules in English):
https://tinyurl.com/yqojpwnx
on 14. January 2024, 18:44 by Lucx
Super Rätsel. Es fängt ganz gemütlich an, aber zum Schluss musste ich nochmal ganz schön knabbern. Für die Lösungscode-Eingabe musste ich dann auch nochmal genau lesen ;-) OK, aber nun ist auch dieses wieder einmal ganz wunderbare Rätsel gelöst und es geht ins Roller-Coaster-mit-Extras-Finale!
on 28. December 2022, 20:14 by polar
@MazzleFlush:
The second options that you gave are correct i.e. each digit along the path alternates.
on 28. December 2022, 19:06 by MazzleFlush
Perhaps another question, in the worm rule, does that mean that along a path, you can find a sum (1,5,6,8) then (8,5,3,2) or is it more like (2,8,4,6) and then (6,9,4,7)? In which way does it alternate?
on 26. December 2022, 17:05 by Uhu
@MazzleFlush: A sum counts till the end of the grid. If the loop goes from R4C5 straight to R4C8, there are 2 sums – the one from R4C56 and from R4C78.
And yes, each quadrant can only have one rule. You can’t have quadrants without a rule and you cannot have a quadrant with two rules. (Additionally, one rule isn't applied at all.)
on 25. December 2022, 22:43 by MazzleFlush
I need some clarification on the ruleset, I think I am having troubles as a result of translation. At which point does a sum on a row or column count? Do the numbers on the corners count as well? If it is LIIL, does the sum consist of the two numbers with a straight path or of the four numbers including the corners? Additionally, someone states that each quadrant can only have one rule, but that is not how I am reading the rules, for me it says each rule has to be applied once, so theoretically all rules could be applied to Q2, or any other division, as long as all 5 rules are all applied once, is this correct?
on 31. May 2022, 20:50 by Alex
Genial!
on 1. April 2022, 15:54 by Uhu
Regeln verdeutlicht. Danke für die Vorschläge, Dandelo und Statistica.
on 31. March 2022, 20:29 by Dandelo
Und daran, dass Ausnahme 2 auch unten rechts gilt, ändert das doch nichts, oder?
Das Problem ist die Formulierung mit "gilt" oder "gelten". Schreib doch einfach "Ordne jedem Diagramm genau eine der folgenden Regeln zu, jede Regel maximal einmal." Dann gibt es genau eine Zuordnung, die funktioniert. Und es ist kein Problem, wenn eine Regel in einem weiteren Diagramm gilt. Dann könnten die alten Formulierungen der Regeln auch bleiben.
on 31. March 2022, 20:20 by Dandelo
Jetzt ist es verschlimmbessert, finde ich. Sollte es nicht heißen:
Der Weg darf sich kreuzen und muss sich auch mindestens einmal kreuzen.
Aber das Rätsel ist großartig.
on 31. March 2022, 19:10 by Uhu
Die Regel bezüglich der gelben Felder verdeutlicht, ebenso dass jede Ausnahme nur maximal einmal gelten darf.
on 31. March 2022, 08:54 by Statistica
Tolles Rätsel. Aber die beiden Regelklärungen ("Problem gelbe Felder" und die Tatsache, dass jede 'Ausnahme' nur einmal gelten darf) würde ich noch irgendwie mit aufnehmen. Habe deswegen auch anfangs ein paar Mal neu angefangen und nur durch das späte Kommentarlesen die Erleuchtung gehabt. Aber jetzt weiß ich Bescheid und kann mich an die große Schwester wagen ;-)
on 6. March 2022, 09:23 by ManuH
So unglaublich genial!!!!
on 5. March 2022, 14:44 by AnnaTh
Waaaaaahnsinn! Super schön und mega tricky. Für den "großen Bruder" muss ich sehr viel Anlauf nehmen.
on 5. March 2022, 13:33 by Uhu
@Dandelo: Ja, genau.
on 5. March 2022, 13:19 by Dandelo
Nur zur Sicherheit:
Das rote Wegsegment in https://tinyurl.com/ycdfdrhl
würde als 2 bzw. 3 gezählt, stimmt das?
on 5. March 2022, 13:18 by zuzanina
Sehr schön! :-)
on 5. March 2022, 10:26 by Lara Croft
Tolles Ding. Knackig, aber absolut machbar. Hat mir richtig gut gefallen. Und gerade habe ich gesehen, wofür das "nur" das Beispiel ist. Oh Hauaha!
on 5. March 2022, 09:03 by ibag
Toll! Ich hab auch hier unzählige Anläufe gebraucht. ;-)
on 4. March 2022, 18:39 by marcmees
trying to get me scared? :-)
on 4. March 2022, 18:29 by Uhu
@marcmees: sorry, this one felt like 3*, after I had worked on the real puzzle :-)
on 4. March 2022, 18:28 by Uhu
Schwierigkeit angepasst.
on 4. March 2022, 18:22 by marcmees
very hard and tricky
(only 3* ?). Maybe it's because I'm recovering from covid but I didn't get the feeling this was "just" a beispiel. Looking forward to the "real" one. :-)
on 4. March 2022, 17:37 by Uhu
@marcmees: yes, exactly. (If you need more clarification or an example, let me know.)
on 3. March 2022, 21:56 by Jesper
Sehr schön. Freue mich auf der Fortsetzung.
on 3. March 2022, 21:27 by Uhu
@ildiko: genau, jede Ausnahme gilt maximal einmal.
on 3. March 2022, 21:24 by ffricke
Huih, war das ein Höllenritt, mir ist noch ganz schwindlig. So oft habe ich mich verfahren und doch am Ende die Runde schließen können. Ich bin mehr als gespannt auf den großen Bruder, von daher war das Training für mich sicherlich notwendig, denn ich hab das Beispiel schon mit 4 Sternen bewertet.
on 3. March 2022, 20:40 by ildiko
Juhu! Freue mich schon auf das Wochenende.
on 3. March 2022, 17:31 by Uhu
@marcmees: You can't mix the rules. There is exactly one rule in each quadrant. For rule 2, the given yellow cell isn't part of the loop (and the loop can't cross itself).
on 3. March 2022, 17:15 by marcmees
@Uhu: thanks for clarification. I got stuck on that one assuming rule 1 and rule 2 couldn't exist together in that quadrant.
on 3. March 2022, 15:59 by Uhu
@marcmees: In the quadrant where the rollercoaster may cross itself, the given yellow cell has no significance for the loop. It can either be part of the loop or outside of the loop.
on 3. March 2022, 15:45 by zuzanina
Hurra, ein neuer Roller Coaster!! Das Beispiel sieht allerdings schon nach einem echten Rätsel aus ;-)