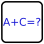Kropki squared sudoku #1
(Published on 20. September 2020, 07:45 by Nylimb)
This is a variant of a kropki sudoku, in which each dot gives information about 4 adjacent cells, not 2.
Standard sudoku rules apply: Fill the grid with numbers from 1 to 9, so that every row, column, and 3x3 box contains each of the 9 numbers exactly once.
For each group of 4 cells that forms a 2x2 square, a black dot in the middle means that the numbers can be divided into 2 pairs (A,B) and (C,D) with A/B=2 and C/D=2. A white dot means that they can be divided so that A‑B=1 and C‑D=1. A grey dot means that they can be divided so that A‑B=1 and C/D=2.
In case 2 different dots could be used, the darkest possible dot will be shown. For example, the numbers 1, 2, 3, and 6 would have a black dot, since 2/1=2 and 6/3=2, not a grey dot (2‑1=1 and 6/3=2). The numbers 3, 4, 5, and 6 would have a grey dot, since 5‑4=1 and 6/3=2, not a white dot (4‑3=1 and 6‑5=1).
Digits can be repeated within a 2x2 square if they're not in the same row, column, or box.
All possible dots are given.
The puzzle is available on Penpa.
Solution code: Row 9 and column 9.
Comments
on 11. November 2022, 15:59 by ndsurgenor
Glad to have finally got this one an official rating!
on 21. October 2020, 01:57 by Nylimb
Added Penpa link.
on 5. October 2020, 16:42 by cdwg2000
@Nylimb
Thank you for your reply. I think I haven’t found a more suitable logical path to solve the problem. I will continue to try the second problem later.
on 5. October 2020, 12:49 by Nylimb
@cdwg2000: Generally speaking, when I'm creating a puzzle I begin with some constraints that allow the solver to get started, and then gradually add more constraints to continue the solution path. In the beginning there are many different choices of constraints that work, but after a while the choices get restricted, and it's more a matter of finding constraints that work rather than designing them. At that point I often use a computer to find all solutions and show the constraints that lead to unique solutions. I then try those by hand to see if they have nice logical paths to the solution. Many of them don't, so I reject them. But some of the rejects may have a constraint that leads to some nice logic, even if it's not enough to fully solve the puzzle without bifurcation. So I add that and run the program again. If I'm lucky, I eventually come up with a puzzle that I enjoy solving.
In this case, I started by looking at 3x3 boxes with 4 dots in them, and came up with the arrangement in box 4 of the puzzle. Then I experimented with adding more dots, picking ones that allowed me to fill in more digits. That led to the arrangement in columns 1 to 3. I think I added another dot or two before running my sudoku solving program for the first time, and when it ran it found millions of solutions and listed the resulting dot patterns. Most patterns gave multiple solutions, so I rejected those. I tried solving some of the remaining ones by hand, starting with ones that had a small number of dots; I think 10 dots was the minimum that I tried. I couldn't see how to solve those without bifurcation, but some of them had additional dots that yielded some nice logic. I ran the program again with those dots added, and again tested some of the results by hand. I found a few that had nice logical solution paths, and decided that this was the best one.
on 5. October 2020, 09:54 by cdwg2000
I am very curious: the logical problem-solving path of the problem itself is very narrow. How did you consider the problem when you set it out, or that there is a particularly hidden problem-solving logic? Thank you!
on 3. October 2020, 06:33 by Nylimb
Clarified rules, added '#1' to name.
on 27. September 2020, 20:07 by Aishasei
Can numbers within a 2x2 square repeat?
@Aishasei: Yes, they could repeat if the square crosses a box boundary.
on 25. September 2020, 18:23 by SudokuExplorer
Wonderful! I really enjoyed the logic :-)
on 21. September 2020, 17:16 by Mody
hat mir gut gefallen