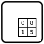
Queens on 7x7 Torus
(Published on 13. August 2020, 00:00 by SudokuExplorer)
Anyone who finds this easy, can try the larger Queens on 11x11 Torus sudoku. If you want a similar puzzle but with a twist, do try my Gossiping Queens on 7x7 Torus puzzle. Below this sudoku, there is also a bonus puzzle to do with this construction. There is also a bonus bonus puzzle about existence. Do give them a try and tell me how you find them (in a hidden comment).
Normal sudoku rules apply (each row, column and region contains the numbers 1 to 7).
We also have the toroidal constraint.
On a torus, when you walk along a row you end up back to the start of that row. Whilst if you climb up a column, you end up back to the bottom of that column. To visualise the regions in this sudoku, you may have to walk/climb through the thick grey lines at the "edges" of the sudoku. The thick black lines are the edges of the regions.
Moreover, every digit has the anti-queen constraint. This constraint is toroidal, meaning that you can move diagonally across the "edges" of the sudoku. For example, in this sudoku, the given digits 5 and 6 are both a queen's move away from 2.
You can try this on Penpa-Edit. Have fun on this torus!
Show that there are two anti-queen patterns on this 7x7 torus (after permutations of the digits 1 to 7).
The above sudoku gives one pattern, what is special about the other one?
Bonus Bonus Puzzle:
Show that if a n x n toroidal sudoku has the anti-queen constraint, then n is coprime to 6.
Hint: Express the anti-queen constraint in the language of permutations modulo n. You might first want to show that n must be odd.
Solution code: Enter the 5th and last rows (left to right).
Comments
on 31. July 2021, 20:32 by SudokuExplorer
Fixed labels/tags
on 21. September 2020, 19:16 by SudokuExplorer
Added toroidal tag (it seems to have magically disappeared)
on 11. September 2020, 19:49 by SudokuExplorer
Added link to recent Gossiping Queens on 7x7 Torus puzzle.
on 4. September 2020, 01:38 by SudokuExplorer
Added link to 11x11 Anti-Queen Toroidal Sudoku
on 16. August 2020, 16:20 by SudokuExplorer
Edited hint of second bonus puzzle
on 14. August 2020, 14:29 by SudokuExplorer
@glum_hippo I have been thinking a bit about an 11x11 version. So far I have two possible 11x11 toroidal anti-queen latin squares (after translation, rotation, reflections and digit permutations). I'll also think about a 13x13 version (to see if I can find more interesting patterns). Maybe I'll try a bit more number theory and see how far I can get, unless anyone else has different ideas to construct such patterns. Be prepared to scream in two weeks time! ;-)
on 14. August 2020, 14:04 by glum_hippo
It's a lovely idea. If I see an 11x11 all-anti-queen sudoku I will scream, however.
on 14. August 2020, 14:01 by SudokuExplorer
Added hint for bonus bonus puzzle.
Do think about the two bonus puzzles.
on 13. August 2020, 21:13 by SudokuExplorer
Added bonus bonus puzzle
on 13. August 2020, 21:08 by SudokuExplorer
@panthchesh Btw I just did a bit of number theory, and managed to show that if a n x n toroidal sudoku has n queens, then n has to be coprime to 6. I was really lucky to construct this 7x7 anti-queen toroidal sudoku :-D
on 13. August 2020, 09:18 by SudokuExplorer
@panthchesh and @aneoid I'm pleased you enjoyed it :-)
I'm trying to make a couple of more approachable puzzles, after my last few harder sudokus. You might see a bigger version in two weeks time (next week I will post my 9x9 killer pentuplet sudoku).
on 13. August 2020, 03:50 by panthchesh
Thanks that was fun! Next time, consider a larger version! :D
on 13. August 2020, 03:31 by aneoid
Thanks for another fun puzzle, SE.