Tigger Bounce Sudoku
(Published on 23. July 2020, 16:40 by mandourin)
The Manhattan distance between two cells is the minimum number of horizontal or vertical steps to go from one cell to the other. It is also the sum of the horizontal gap and the vertical gap between these cells. For example, the Manhattan distance between R1C3 and R4C8 is 3+5 = 8.
A Tigger Bounce is a move between two cells at a Manhattan distance of 5. The term was coined by Simon Anthony in this video.
This puzzle obeys the usual Sudoku rules: every column, every row and every outlined 3x3 boxes contain each digit from 1 to 9 exactly once.
An additional constraint is that two cells separated by a Tigger Bounce must contain different digits.
Credits to ryokousha for discovering the only two possible configurations satisfying the Tigger Bounce constraint.
To solve online on f-puzzle.
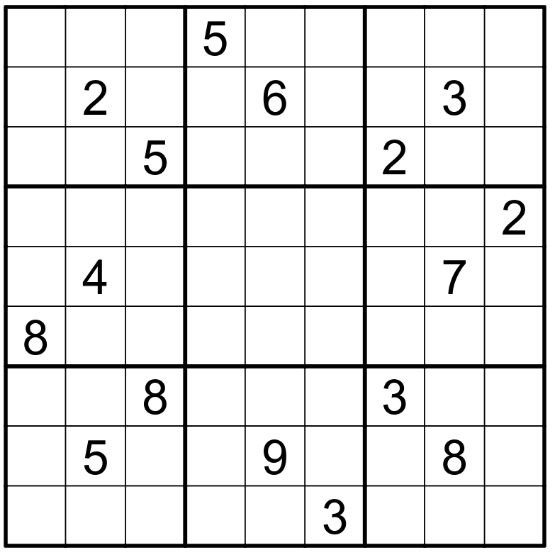
A Tigger Bounce is a move between two cells at a Manhattan distance of 5. The term was coined by Simon Anthony in this video.
This puzzle obeys the usual Sudoku rules: every column, every row and every outlined 3x3 boxes contain each digit from 1 to 9 exactly once.
An additional constraint is that two cells separated by a Tigger Bounce must contain different digits.
Credits to ryokousha for discovering the only two possible configurations satisfying the Tigger Bounce constraint.
To solve online on f-puzzle.
Solution code: Row 8 followed by column 6 (without separator).
Solved by Greg, glum_hippo, SirWoezel, marcmees, RockyRoer, saskia-daniela, wilsig, SKORP17, checkoway, Lifaja, Bismuth, washyleopard, sirtramola, absolutebeginner, TheSchnei, Toastbrot, NikolaZ, Quarterthru, ... Thomster, Mathi, ManuH, Uhu, keelyc27, jgarber, morgannamodeaura, Cane_Puzzles, Raistlen, ParaNox, pwinn, Rollie, PinkNickels, Overhead, zrbakhtiar, metacom, Jordan Timm, Carolin, Crul, drf93, NEWS
Comments
on 24. July 2020, 23:47 by SlowLarry
So in theory it should be uniquely solvable with only 8 different givens. Question is if this is human-solvable.
on 23. July 2020, 17:49 by glum_hippo
I don't know how many times I tried to scan 4 steps as 5, but I guess I'm not a cartoon tiger! :-)


