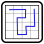
Yajilin Sudoku
(Published on 19. July 2020, 12:39 by Madmahogany)
This puzzle is a combination of a Yajilin puzzle and Sudoku
Yajilin Rules: You need to place some blocks in the grid. The grey cells are clues for the number of blocks in the given direction. Blocks cannot touch orthogonally. The remainder of the grid (not blocks or clues) must be a part of a single continuous non-intersecting loop. The answer code will involve the length of horizontal/vertical loop segments in a row/column respectively. This is the number of cells the loop travelled along that row or column until it turned out of it. Multiple loop segments are represented separately (i.e. if the loop goes one cell along the row, leaves and returns to the row and goes 4 cells, the answer would be 14, not 5)
Sudoku Rules: Normal Sudoku rules apply. The digits present in the grey cells act as the Yajilin clues. Also, the loop can only turn in an odd cell.
Here's the Penpa-Link for solving
Solution code: The length of horizontal loop segments in Row 2 (separate loop segments written separately), followed by the length of vertical loop segments in Col 2 (separate loop segments written separately), followed by the digits in Row 2, then Col 2
Comments
on 21. July 2020, 11:22 by Madmahogany
@Jesper @japoorva Thank you!
on 21. July 2020, 06:17 by japoorva
Great Puzzle! @Lizzy01 Thanks for the comment. That was helpful for entering the solution code!
on 20. July 2020, 21:14 by Jesper
A very nice concept - I really enjoyed this puzzle!
on 20. July 2020, 11:36 by Madmahogany
@Nylimb Thank you!
on 20. July 2020, 11:26 by Nylimb
@Madmahogany and @Lizzy01: Thanks for the clarification. I never would have thought of that.
@Madmahogany: Thanks for the nice puzzle.
on 20. July 2020, 11:05 by Madmahogany
Updated solution code, and clarification of Yajilin solution code
on 20. July 2020, 10:00 by Lizzy01
@Nylimb I had some trouble with this too. It turned out it's the lengths in segments per part of the path, so if there were to be 3 parts, one of length 1, one of length 5, and another of length 1, that part of the code would be 151, not 7 or 3. (using random example cuz i don't know how to make only you see this)
on 20. July 2020, 00:40 by Madmahogany
@zhergan Thank you!
on 19. July 2020, 23:23 by zhergan
Brilliant idea! Thanks:)
on 19. July 2020, 20:41 by glum_hippo
@henrypijames - Yajilin loops can and in fact must touch themselves orthogonally, so no, it's not quite like a snake.
on 19. July 2020, 15:10 by henrypijames
Is the "single continuous non-intersecting loop" basically a one cell wide snake biting its own tail (aka a ouroboros)?
@henrypijames Yes, it should be a closed loop.
on 19. July 2020, 13:05 by Madmahogany
Penpa link