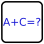Logic Masters Deutschland e.V.

This puzzle combines features of X-sums and sandwich sudokus.

First, standard Sudoku rules apply: Fill the grid with numbers from 1 to 9, so that every row, column, and 3x3 box contains each of the 9 numbers exactly once.

Second, a number to the left of a row shows the sum of all numbers in the row between the X-th cell from the left end and the Y-th cell from the right end, where X is the number at the left end and Y is the number at the right end. Numbers above columns work similarly. Here are a few examples:

If a row has 246918753, then X=2 and Y=3. The X-th number from the left is 4 and the Y-th number from the right is 7, so the clue for the row would be 6+9+1+8 = 24.

If a row has 719283546, then X=7 and Y=6. The X-th number from the left is 5 and the Y-th number from the right is 2, so the clue would be 8+3 = 11.

If a row has 548973216, then X=5 and Y=6. The X-th number from the left is 7 and the Y-th number from the right is 9. There's nothing between 7 and 9, so the clue would be 0.

If a row has 492578316, then X=4 and Y=6. The X-th number from the left and the Y-th number from the right are both 5, so again the clue would be 0.

If there's no clue next to a row or column, then the sandwich sum can be anything.

I haven't seen this type of puzzle before, but I wouldn't be surprised if it's been invented before. If you know of a previous example, please post a comment about it.

To answer my own question, this puzzle is very similar to 3 puzzles that were published here recently, Battlefield Sudoku #1 and Battlefield Sudoku #2 by Big Tiger and Battlefield Sudoku by Realshaggy. I hadn't noticed those until after publishing this one. I hope that having 2 such similar puzzle types won't be too confusing!

The puzzle is available on Penpa.