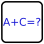Parity Party IX - "Square-ity Party"
(Published on 13. May 2020, 06:30 by glum_hippo)
Update: this puzzle is now available in the CtC app here. This puzzle was changed in mid-January.
Parity Party IX
Normal Sudoku rules apply.
»Parity Party« Rules: A number at the edge of the grid indicates the sum of cells encountered when moving through the grid from that vantage point, UP TO AND INCLUDING the first odd or first even digit. For example, a 15 at the bottom of a column could indicate something like 7-8, 8-7, 1-3-5-6 or 2-6-4-3 (among others) when reading up that column... but not 1-2-3-4-5 or 2-6-3-4 etc. That is, the parity of the farthest digit must deviate from that of the others.
Note: If the clue is less than 10, it might simply indicate the value of the first cell. That is to say, you could be adding up zero odd and one even number, or vice versa.
Additional constraint: The grid contains three 3x3 'magic squares' (Wikipedia) with 9 unique digits, whose position, size and orientation (i.e., they could be at any angle!) remains to be determined. Each framed cell lies on at least one vertex/edge/center of a magic square. Here is a (non-exhaustive) list of possible example positions for the magic squares. The vertices/edges/centers are purple dots:
Solution code: The 8th column and then the 5th row, in conventional reading order (18 digits total)
Comments
on 5. March 2023, 10:54 by PixelPlucker
Refreshingly different, thanks! And after 2.5 years of sporadic engagement, I finally get to put a bow on one of the first puzzle series I explored on this site.
Slightly bittersweet of course, but thanks for them all, and I hope there will be more to come (repetition does legitimise) :)
on 14. January 2023, 16:12 by glum_hippo
One of the grey squares was moved in order to bypass an unpleasantly complicated step
on 4. February 2022, 13:31 by Vebby
I got absolutely beaten by this one, the puzzle hit me with a Confundus Charm. Completely overlooked some possibilities for magic squares initially, but thanks to some kind and patient assistance from glum_hippo I finally spotted them. Rest of the puzzle solves smoothly.
on 19. May 2020, 18:53 by glum_hippo
@Madmahogany Each framed cell is one of the 9 members of a magic square. EDIT: The way the rule is formulated, it is NOT ruled out that a framed cell lies on more than one magic square.
on 19. May 2020, 18:36 by Madmahogany
Just a clarification, the framed cells have to lie in one of the three magic squares?
