Rätsel im Advent (15): Schneemann
(Published on 15. December 2015, 09:00 by usp)
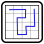
Find three paths with lengths 8, 18 and 24 that have been freed from snow when Santa Claus' helpers build a snowman. The paths connect vertically or horizontally adjacent cells and end near the cell with the snowman. The paths do not touch each other, not even diagonally, except near the snowman. Numbers at the edge of the grid determine how many cells in the respective row or column are free from snow.
Solution code: For every row from top to bottom the length of the longest segment of any path
Comments
on 29. December 2020, 23:36 by KarinAnna
Bitte wer hat die Lösung oder kann mir sagen in welchem Kästchen der längste Weg beginnt! :-)
on 13. December 2020, 14:59 by Dontknow
Ich sitze jetzt seit 8 Tagen an diesem Rätsel und verzweifel langsam :( hat jemand eine Tipp für mich?
on 11. January 2016, 23:03 by pin7guin
Lustig: Ich habe mein 24. Adventsrätsel als 24. gelöst. ;-)
Ansonsten schließe ich mich meinem Vorredner an...
on 16. December 2015, 08:03 by Statistica
Also - für mich - WIRKLICH knifflig. Schlangen und ich, wir werden keine Freunde mehr...
on 15. December 2015, 20:20 by usp
Richtig. Man könnte sagen, ist es also mit dieser Zählart viel weniger knifflig als mit einer anderen, da die anderen unlösbar sind ;-)
on 15. December 2015, 18:20 by HaSe
Daher auch Summe der leergefegten Felder 50
on 15. December 2015, 10:40 by dm_litv
Knifflig!
on 15. December 2015, 10:24 by Luigi
@usp: Danke! Dann ist dieses Rätsel kniffliger als erwartet.
on 15. December 2015, 10:21 by usp
Kästchenzahl = Länge. Wie bei einer Schlange.
on 15. December 2015, 09:44 by Luigi
Hat ein Pfad über zwei Kästchen per Definition die Länge 2 oder die Länge1?
Bzw. Ist die Länge eines Pfades mit der Anzahl benutzter Kästchen identisch?