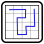
Odd Tapasyu
(Published on 29. October 2014, 00:00 by usp)
Apply the rules of variable Tapasyus (see below).
In this puzzle the information on clues is incomplete, but every clue is non-zero. Every 0 has to be replaced by an even number, every 1 by an odd number. Question marks symbolize arbitrary numbers.
Draw a closed loop into the grid. It must go from the center of one cell to the center of a horizontally or vertically adjacent cell, passing every cell at most one time.
The loop uses every cell with a circle. Circles may be blackened. In white circles the loop keeps straight on but bends in at least one of the adjacent cells (following the loop). In black circles the loop bends but keeps straight on in both adjacent cells.
The loop must not pass cells containing numbers. A number determines how many of the neighbouring cells are used by the loop. These cells must form a group not interrupted by empty cells, but need not to be a contiguous part of the loop. Distinct groups of loop cells around the same numeric cell must be partened by at least one empty cell.
Solution code: The number of black circles in each letter made of Masyu circles, followed by the lengths of all horizontal lines in the middle row.
Comments
on 26. November 2014, 17:51 by HaSe
again: herausragend
on 3. November 2014, 13:50 by usp
@zorant: 1 can also be replaced by 1 (this is an odd number, too).
on 3. November 2014, 12:32 by ffricke
Mir gings erst wie Gabi, aber dann sah ich den Einstieg und es lief flüssig. Diese Tapasyus sind ein Genuss!
on 2. November 2014, 19:28 by zorant
Hi,
Does the number 1 can only be replaced with 3,5,7 or can remain "1"?
on 2. November 2014, 08:42 by ibag
Großartig!!! Am Anfang dachte ich, da geht gar nichts ...
on 29. October 2014, 12:31 by Katrin K
Einfach toll!
on 29. October 2014, 05:19 by r45
Noch mehr suuuuper! ;-)