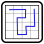
Polyominos
(Published on 30. April 2014, 20:00 by tuace)
Schwärze einige Felder und zeichne auf diese Weise einige Polyominos (Flächen aus beliebig vielen orthogonal zusammenhängenden Felder) in das Diagramm, und zeichne ferner in alle nicht geschwärzten Felder einen geschlossenen Rundweg, der orthogonal von Feldmittelpunkt zu Feldmittelpunkt verläuft, sich nirgends kreuzt und jedes fett umrandete Gebiet genau einmal betritt und wieder verlässt. Kein Polyomino darf dabei mehr als einmal verwendet werden, auch, wenn man es dreht oder spiegelt, und kein Polyomino darf ein anderes berühren, auch nicht diagonal.
Die Anzahl der fett umrandeten Gebiete, in denen sich ein Polyomino befindet, bestimmt immer auch die Mindestanzahl der Felder, die das Polyomino in jedem Gebiet belegen muss. Befindet es sich also z.B. in zwei Gebieten, müssen in beiden Gebieten mindestens zwei Felder zum Polyomino gehören.
Solution code: Die Anzahl der Felder, in denen der Rundweg abknickt, zeilenweise von oben nach unten.
Comments
on 26. October 2022, 18:11 by polar
Brilliant construction.
on 11. August 2021, 06:31 by tuace
+ Label "Polyominos"
on 8. April 2019, 18:48 by r45
@jessica6: Vollständig geschwärzte Gebiete kann es meines Erachtens nicht geben. .... "und jedes fett umrandete Gebiet genau einmal betritt und wieder verlässt."
on 8. April 2019, 16:59 by jessica6
Muß der Rundweg eigentlich jedes Gebiet betreten, oder nur jedes Gebiet mit mindestens einem nicht geschwärzten Feld (d.h. kann es auch vollständig geschwärzte Gebiete geben?)
on 17. February 2016, 09:23 by AnnaTh
Hartnäckigen Denkfehler beseitigt: danach war's einfach nur noch toll!
on 2. September 2015, 13:41 by sandmoppe
Erst steht man da, wie die Öchsin vor dem Berg. Doch nach genauerer Betrachtung des Berges, hat jetzt auch diese Öchsin ihren Weg drumherum gefunden.
Tolles Rätsel! Hat viel Spass gemacht. Die größte Hürde für diese spezielle Öchsin war das Wörtchen "maximal".
on 26. April 2015, 08:37 by tuace
@Peter Luzifer: Jedes einzelne Polyomino, das sich in N Gebieten befindet, muss sich in jedem dieser Gebiete aus mindestens N Felder zusammensetzen, unabhängig davon, ob noch ein anderes Polyomino diese Gebiete "nutzt".
on 26. November 2014, 00:42 by pin7guin
Ich wusste überhaupt nicht, wo ich hier hätte ansetzen können...
Uvo hat mir auf dem Rätselwochenende einen Tipp gegeben. Axel und ich haben uns dann Schritt für Schritt durchgearbeitet.
on 18. August 2014, 12:24 by tuace
@RALehrer: Your rules are correct. ;)
on 18. August 2014, 06:30 by RALehrer
I think I might have some wrong rules:
Each area must be entered exactly once, much like country roads (implying there must be at least one empty square per region).
If a polyomino spans N regions, then it must include at least N cells in each region (i.e., size at least N^2).
No polyomino can be repeated in the diagram, so there is at most 1 singleton, 1 doubleton, 2 triminos, 5 tetronimos,...
on 16. May 2014, 01:58 by kiwijam
Very nice rules, I'm surprised how well it works :)
on 11. May 2014, 16:02 by Mody
Großartige Rätselidee :)
on 7. May 2014, 08:24 by Statistica
Ganz klasse!
on 5. May 2014, 19:17 by tuace
Label ergänzt; war mir erst nicht sicher, ob man hier NEU setzen kann, aber in Anbetracht der Kommentare... :)
on 5. May 2014, 09:44 by CHalb
Für mich ein neuer Rätseltyp. Wirklich sehr schön, wie beim Lösen so langsam die Informationsgehalte der Gebiete immer deutlicher werden.
on 4. May 2014, 18:09 by ibag
Wunderbare Konstruktion!
on 3. May 2014, 14:41 by tuace
Danke Euch für die Blumen :)... ich hatte nämlich erst noch lange überlegt, ob ich es überhaupt veröffentlichen sollte...
on 3. May 2014, 10:57 by Luigi
Am Anfang habe ich hilflos herumgestochert und habe immer wieder gezweifelt, ob sich dieses Rätsel wirklich logisch lösen ließe.
Aber wenn man sich in dieses Rätsel erst einmal reingedacht hat ist es einfach nur schön und genial konstruiert.
on 3. May 2014, 10:23 by Alex
super konstruiert! Ich musste meine grauen Zellen gehoerig anstrengen.
on 3. May 2014, 00:02 by pokerke
Wow, great puzzle. Amazing how this puzzle combines old elements in a completely new way. I really enjoyed it a lot. Thanks!