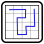
Gekoppelte Roboterwege
(Published on 8. January 2013, 05:48 by MiR)
|
In the red circle of each grid is standing a robot, which starts there to traverse a closed path for ever and ever. The respective path passes each cell exactly once and connects orthogonally adjacent cells. In the centre of each cell of both grids is a contact switch, which controls the direction of the respectively other robot until its next cell centre. The robots move alternately until the respectively next cell centre. Robot A makes the first step; robot B moves for the first time after robot A reaches its next cell centre. Some route indicators of the switches are prescribed. Which pathes do the robots go? How are the single route indicators of the switches? Here is an example, in which all route indicators are already prescribed: To this puzzle I was inspired by:
|
Solution code: For grid A the count of knees of the path and the route indicators (N, O, S, W) on the top left starting diagonal. Then the corresponding dates for grid B.
Last changed on on 7. March 2013, 10:36
Solved by pokerke, ibag, Luigi, Zzzyxas, ildiko, moss, Toastbrot, Mody, BFaw, Alex, zorant, rimodech, jirk, dm_litv, pirx, matter, relzzup, tuace, ch1983, Joe Average, sandmoppe, AnnaTh
Comments
on 9. March 2013, 10:51 by dm_litv
Very interesting logic!
on 7. March 2013, 10:36 by MiR
Layout-Änderungen. Layout-changes.
on 8. January 2013, 12:23 by Luigi
Sehr schönes und anspruchsvolles Rätsel!
Wie Kim schon sagte, man kann sehr einfach zwischen den beiden Rastern verloren gehen.
on 8. January 2013, 09:40 by MiR
@pokerke: Thanks for your early solution and your comment!
on 8. January 2013, 09:24 by pokerke
It takes a lot of concentration to make sure you don't get lost somewhere between the two grids, but it is a very fun and original puzzle! Thanks!
