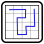
Slalom mit Torstangen, Teil 3
(Published on 15. September 2012, 18:30 by pirx)
Zeichnen Sie in jedes Feld eine diagonale Wand so ein, dass keine vollständig umschlossenen Innenräume entstehen. Die Zahlen in den Kreisen geben an, wie viele Wände von diesem Kreis ausgehen.
Es gelten folgende Zusatzbedingungen:
Ein Slalomfahrer startet im Kreis "S" (Start, oben mitte) und durchquert auf seinem Weg zum Kreis "Z" (Ziel, unten mitte) jedes Tor genau einmal.
Ein Tor
- besteht aus genau zwei Torstangen (graue gefärbte Kreise mit einer roten Umrandung). Jede Torstange ist Teil genau eines Tores,
- ist genau zwei Felder breit,
- liegt entweder horizontal oder vertikal.
Es ist Teil des Rätsel herauszufinden, welche Torstangen zusammen ein Tor bilden, und in welcher Reihenfolge der Slalomfahrer die Tore durchquert.
Eine Beispielaufgabe findet sich in Teil 1.
Und hier das Rätsel:
Solution code: Die Länge des Slalomweges gefolgt von der Anzahl der Wände, die vom Startkreis, von jeder Torstange und vom Zielkreis ausgehen. Reihenfolge: Startkreis, linke und dann rechte Torstange des ersten durchquerten Tors aus Sicht des Slalomfahrers, linke und dann rechte Torstange des zweiten durchquerten Tors aus Sicht des Slalomfahrers, usw.
Comments
on 24. September 2012, 08:55 by ibag
Danke für die tolle Serie! Ich habe viel über Slaloms dazugelernt. Und dieses hier mit seinen Symmetrien gefällt mir besonders gut.
on 16. September 2012, 22:36 by Alex
Danke fuer diese tolle neue Serie. Hat mich ganz neue Schluesse ziehen lassen.
on 15. September 2012, 22:34 by Zzzyxas
Sehr schön!