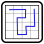
Slalom mit Torstangen, Teil 2
(Published on 15. September 2012, 18:30 by pirx)
Zeichnen Sie in jedes Feld eine diagonale Wand so ein, dass keine vollständig umschlossenen Innenräume entstehen. Die Zahlen in den Kreisen geben an, wie viele Wände von diesem Kreis ausgehen.
Es gelten folgende Zusatzbedingungen:
Ein Slalomfahrer startet im Kreis "S" (Start, oben links) und durchquert auf seinem Weg zum Kreis "Z" (Ziel, unten rechts) jedes Tor genau einmal.
Ein Tor
- besteht aus genau zwei Torstangen (graue gefärbte Kreise mit einer roten Umrandung). Jede Torstange ist Teil genau eines Tores,
- ist genau zwei Felder breit,
- liegt entweder horizontal oder vertikal.
Es ist Teil des Rätsel herauszufinden, welche Torstangen zusammen ein Tor bilden, und in welcher Reihenfolge der Slalomfahrer die Tore durchquert.
Eine Beispielaufgabe mit Lösungscode findet sich in Teil 1.
Und hier das Rätsel:
Solution code: Die Länge des Slalomweges gefolgt von der Anzahl der Wände, die vom Startkreis, von jeder Torstange und vom Zielkreis ausgehen. Reihenfolge: Startkreis, linke und dann rechte Torstange des ersten durchquerten Tors aus Sicht des Slalomfahrers, linke und dann rechte Torstange des zweiten durchquerten Tors aus Sicht des Slalomfahrers, usw.
Comments
on 9. February 2020, 09:06 by Dandelo
Bin zufällig auf diese alte Serie gestoßen. Sehr schöne Variante, eigentlich macht der Name erst damit Sinn.
Und bei der Suche nach dem logischen Weg kamen mir Erkenntnisse, die auch bei der Standard-Variante helfen dürften.
on 21. September 2012, 10:03 by CHalb
Wenn ich ein ganzes Tor im Lösungscode vergesse, kann's ja nicht gehen.
Toll konstruiert! Ich finde den Unterschied zwischen Standardslalom und dieser Variante ähnlich wie zwischen Standardsudoku und Chaossudoku. Nur eine kleine Änderung bringt deutlich mehr Möglichkeiten und damit Abwechslung.
on 19. September 2012, 10:43 by Statistica
Das hat ein wenig länger gedauert, den logischen Weg zu finden. Klasse, danke für die Serie!
on 17. September 2012, 04:33 by saskia-daniela
Schöne Serie!
on 16. September 2012, 20:25 by r45
Tolle Konstruktion, hat sehr viel Spaß gemacht, die Serie. Gerne mehr davon.